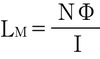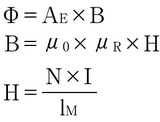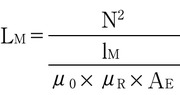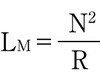メディア

基礎から見直すコイル/トランス：よりよいスイッチモード電源を実現するために（1/3 ページ）

コイルやトランスは、スイッチモード電源などの設計において非常に重要な位置を占める。こうした磁性部品を正しく理解するには、磁気学の知識が必要不可欠だ。しかし現在では、理工系の大学であっても、磁気学に関して実用的なレベルでの指導が十分に行われていないと言われている。本稿では、磁気学の基礎と、コイルやトランスの設計/選択に必要な知識についてひととおり述べる。その上で、スイッチモード電源向けの選択にあたって考慮すべき点を説明する。

» 2010年03月01日 00時03分公開

[Sameer Kelkar（米Power Integrations社），EDN]

押さえておきたい基礎事項

　1831年、英国の化学者/物理学者であったMichael Faraday氏が現在のトランスを発明、彼はそれを誘導コイルと名づけた。それから180年近くたった今、残念ながら理工系の大学でも、SMPS（スイッチモード電源）を扱う上で実用的なレベルでは、磁気学に関する指導があまり行われていないという。問題の1つは、磁気学で扱われる一般的な理論式が正弦波を対象としたものであるのに対し、SMPSは方形波で動作する点にある。

　システム設計においては、電源のことが後回しになるケースがある。しかし、SMPSの中心にある磁性部品を適切に選択し、電源回路全体を適切に設計するのは非常に重要なことである。そこで本稿では、見落とされがちなこの分野の基本を再度確認しておきたい。以下では、まず最低限、頭に入れておくべき基本的な事項について述べる。

■磁界と電流

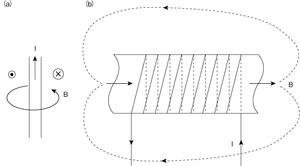
図1 単純な空芯コイルにおける電流と磁界　導体に電流が流れると磁界が生じ、その磁界が導体の周りに磁束線を生成する（a）。導体が複数回巻いてあるコイルに直流電流が流れると、それぞれのターンが磁界を生成する（b）。

　磁気学について理解するための第一歩は、磁界と電流の関係を知ることである。導体に電流Iが流れると、磁界Bが生じ、その磁界が導体の周りに磁束線を生成する（図1（a））。図1（b）は単純な空芯コイルの例を示したものである。導体が複数回巻いてある（ターン）コイルに直流電流が流れると、それぞれのターンが磁界を生成する。すべての磁界が組み合わさった結果、コイル内には直線的な磁界が形成される。コイルの外では磁界は分散して弱まる。最大のエネルギーを蓄えることができるのはコイル内の磁界だが、外側でもかなりの量を蓄えることができる。

　鉄などの磁性材料で構成された物体をコイル内に配置すると、磁界はその物体に対して起電力（EMF：Electromotive Force）を発する。磁界の中に2つ目のコイルを配置し、時間とともに磁界が変化するように1つ目のコイルに交流電流を流すと、磁界は2つ目のコイルに電流を生じさせる。ロシアの科学者/物理学者であるHeinrich Lenz氏が1834年に発表したレンツの法則のとおり、発生する電流の向きは、それを発生させた物体の動きと常に逆方向になる。

　磁界の性質は、強さや密度で表すことができる。磁界の強さHは、アンペア毎メートル（A/m）を単位とし、磁界が磁極に及ぼす力に相当する。磁束密度B は、磁界が変化するときに電界を発生する能力のことで、テスラ（T）を単位とする。磁束密度は時間も関連する概念である。

　磁性部品と、それを利用した機器で観測される特性のほとんどの関係は、アンペールの法則とファラデーの法則の2つで表すことができる。フランスの物理学者 /数学者、Andre-Marie Ampere氏が1826年に発表したアンペールの法則は、閉回路の周囲の磁界と、閉回路を流れる電流の関係を表すものである。前出のFaraday氏が 1834年に発表したファラデーの法則は、発生する起電力または閉回路における起電力が、回路を通る磁束の時間変化率に比例するというものである。

■透磁率

表1 磁気/電気の用語の対応表　

　磁気回路になぜコアが必要なのかという疑問に答えるには、透磁率という特性について考察する必要がある。透磁率とは、物質の単位面積を通過することができる磁束量のことである。図1（b）のコイルは、電磁石と同じように利用することはできない。コアがないからである。しかし、コイルの中にコアとして鉄芯を入れると強力な電磁石となる。鉄の透磁率は真空の約1万倍で、コイルの中にかなり多くの磁束を収束することができるからだ。

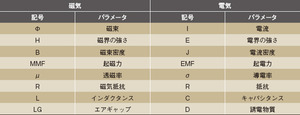
　透磁率は、電気の世界の導電率と同じようなものだと考えることができる。表1は、磁気と電気の世界で使われる用語を対応付けて示したものである。導体が、電流という形でエネルギーを通す物体であるのと同様に、透磁率の高い磁性材料は、磁束という形でエネルギーを通す物体だと考えればよい。

　磁気回路では、リークについて考慮することが重要である。上述したように、電気と磁気の世界には、似たような概念が多く存在する。ただし、真空を基準にした場合、銅などの一般的な導体の導電率は約10²⁰で、約10⁴という磁性材料の透磁率よりもずっと高い。このため、低周波システムにおいて、リーク電流は無視することができてもリーク磁束を無視することはできない。なお、確かに透磁率は導電率に似ているが、多くの物質において線形的な特性ではない。

■BH曲線とヒステリシス

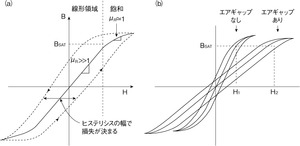
図2 ある強磁性材料のBH曲線　磁界の強さHと磁束密度Bの間の関係を表している（a）。磁界が弱い場合、透磁率は一定で比較的高い。エアギャップを導入すると、BH曲線は右に傾く（b）。

　図2（a）は、ある強磁性材料における磁界の強さHと磁束密度Bの関係を示したものである。BH曲線と呼ばれるこの曲線の傾きが、この材料の透磁率μRとなる。磁界が弱い場合には、透磁率は一定で比較的高い。しかし磁界が強くなると、透磁率は低下し始め、そのうち真空と同じ値（μ_R≒1）にまで低下する。この点を、飽和磁束密度と呼ぶ。この点に達すると、磁束密度を少し上げるだけでもかなり強い磁界が必要となる。

　この物質にはエネルギーを蓄えることができるわけだが、飽和点の状態から磁界の強さが弱まると、物質からエネルギーを復元することができる。しかし復元されるエネルギーは蓄積したエネルギーよりも少なくなる。そのため、磁界を弱めたときのBH曲線は磁界を強めたときとは異なる経路をたどることになる。その結果、1つのサイクルを通したBH曲線は閉じたSの形のヒステリシス曲線となる。ヒステリシス曲線に囲まれた領域は、そのサイクルにおける総損失エネルギーを表す。ヒステリシス曲線の面積は周波数の関数となり、周波数が高いほど面積は増大し、それに伴って損失も増えることになる。

■磁束リンケージ

　総磁束、つまり磁束リンケージは、電流とインダクタンス定数に依存し、以下のように関係を表すことができる。