ポリフェーズフィルタの基本を知る：FIRフィルタの効率的な実装手法 （1/3 ページ）

アップ/ダウンサンプリングに代表されるデジタル信号処理では、多くの場合、FIRフィルタが利用される。FIRフィルタでは、タップ数を増やせば優れた応答特性が得られるが、ロジック回路の規模や消費電力が増えてしまうことが問題になるケースもある。例えばFPGAでは、ポリフェーズフィルタの考え方を導入することで、こうした問題に対処することが可能になる。

[Ron Warner （米Lattice Semiconductor社），EDN]

複数のサンプリングレート

　デジタル信号処理は、MP3プレーヤや携帯型ワイヤレス端末など、あらゆる電子システムで使われている。そして、こうした電子システムの中には、複数のサンプリングレートを使用するものがある。例えば、プロ用オーディオのデータから民生用途向けのデータへの変換など、あるレートでサンプリングした信号を、異なるレートで動作するほかの処理向けに変換しなければならないケースが存在するのだ。このような場合、必要に応じて異なるサンプリングレートのデータを生成しなければならない。

　あるいは、既存のサンプリングデータを再利用するアプリケーションがあり、元のサンプリングレートがそのアプリケーションの要件よりも高いということがある。このような場合には、サンプリングレートを下げたデータを生成し、それに対して処理を施すようにすれば、データのスループットやメモリーリソースに対する要件を緩和することができる。さらには、消費電力を削減し、処理効率を向上させることも可能だ。

　そして、このようなサンプリングレートの変更処理において要となるのがデジタルフィルタである。中でも、FIR（有限インパルス応答）フィルタは特に重要な役割を果たす。FIRフィルタでは、タップ数が多いほど、フィルタとしての応答特性が良くなる。ただし、この点にはトレードオフが存在する。タップ数が多くなると、必要なロジック回路、演算量、消費電力、飽和/オーバーフローの可能性が増大してしまうからだ。

　例えば、FIRフィルタをFPGAで実現する場合、本稿で紹介するポリフェーズフィルタの構成で実装すれば、少ないロジック回路でタップ数の多いものとすることが可能である。しかも、演算量、消費電力、飽和/オーバーフローの可能性を低減することもできる。

ダウンコンバージョン

図1 ダウンコンバージョンの対象とする信号　

図2 サンプルを捨てた結果　4つのサンプルごとに3つを捨てることで、新しい信号のサンプリングレートはF/4となる。

図3 間引き用のローパスフィルタ　サンプルを捨てる前に、信号にフィルタをかける必要がある。

　まず最初に、サンプリングレートを下げるケース、すなわちダウンコンバージョン（Down Conversion）について考えてみよう。

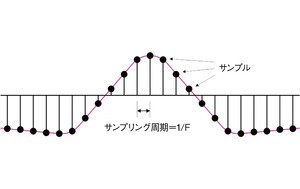
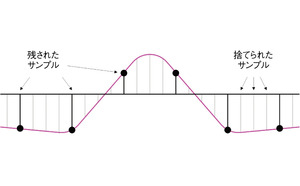
　周波数F（単位はHz）でサンプリングされた信号データ（サンプル）があったとする（図1）。このサンプリングレートを元の周波数の1/4に下げたいとしよう。これを行うための1つの方法は、単純に、元のサンプル4つにつき、3つずつを捨ててしまうことだ（図2）。

　ただし、このようにして一部のサンプルを捨てる場合、最終的に得られる信号にはエイリアスの影響が現れる可能性がある。後にそのサンプリングデータを利用する際、本来は存在しなかった余分な成分が含まれてしまい、それを除去することができなくなるのである。

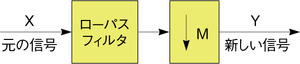
　例として、可聴帯域外の高周波成分を含む音楽信号をA-Dコンバータでサンプリングするケースについて考えてみる。このとき、低すぎるレートでサンプリングし、その後、D-Aコンバータを使って音楽を再生すると、可聴帯域外の高周波成分のエイリアスが可聴帯域内に現れ、余計な音が聞こえてしまうことがある。このようなエイリアスの問題は、A-Dコンバータでサンプリングする前に、不要な高周波成分をローパスフィルタで除去することで回避する（図3）。そして、実は、この低すぎるレートでサンプリングするという処理は、図2の方法でいくつかのサンプルを捨てるのと同じことに相当する。つまり、サンプルを捨てる場合にも、その前にフィルタリングを行う必要があるということだ。

　一般的に、フィルタリングを行わずに、サンプルを捨てる処理だけを行うことを「ダウンサンプリング（Down Sampling）」と呼ぶ。これに対し、フィルタリングを行ってからサンプルを捨てる処理のことを「間引き（Decimation）」と呼ぶ。ただし、実際には、ダウンサンプリング、間引き、ダウンコンバージョンの3つは、同義語として使用されることが多い。

　間引きの処理において、出力サンプリンレートに対する入力サンプリングレートの比率のことを、間引き係数（Decimation Factor）と呼ぶ。上に挙げた例では、入力サンプリングレートは出力サンプリングレートの4倍なので、間引き係数Mは4である。

アップコンバージョン

図4 アップコンバージョンの対象とする信号　

図5 サンプルの補間　値が0のサンプルを補間することにより、信号のサンプリングレートを上げることができる。

図6 フィルタによる処理　最終的な信号のサンプリングレートは4×Fとなる。しかも、余分な信号成分を含まない。

図7 補間用のローパスフィルタ　値が0のサンプルを挿入してから、信号にフィルタをかける。

　次に、サンプリングレートを上げる処理、つまりはアップコンバージョン（Up Conversion）について考える。これが必要となる典型的な例は、システムのほかの部分がより高いサンプリングレートで動作しており、元の信号よりも高いサンプリングレートのデータのほうが処理しやすいというケースである。

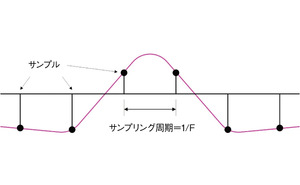
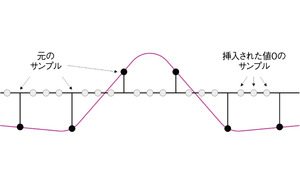
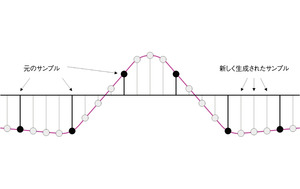
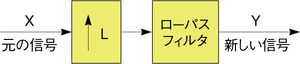
　図4に示したように、周波数F（単位はHz）でサンプリングした信号があったとしよう。このサンプリングレートを元の4倍にしたいケースを考える。それには、元のサンプルの間に、値が0のサンプルを3つずつ挿入すればよい（図5）。しかし、このままではダウンコンバージョンの場合と同様に問題が生じる。新しく加えたサンプルにより、信号に不要な成分が加わることになるからだ。この問題を解決するには、サンプルを追加した後に、新しい信号にフィルタをかけて不要な成分を除去して、より適切なサンプルを生成すればよい（図6）。この場合も、補間用のローパスフィルタ処理を施すことになる（図7）。

　値が0のサンプルを挿入するだけの処理のことを「アップサンプリング（Up Sampling）」と呼ぶ。これに対し、「補間（Interpolation）」は、値が0のサンプルを挿入し、さらにフィルタリングを行う処理のことを指す。実際には、アップサンプリング、補間、アップコンバージョンの3つは同義語として使用されることが多い。

　補間の処理において、入力サンプリングレートに対する出力サンプリングレートの比率のことを補間係数（Interpolation Factor）と呼ぶ。上記の例では、出力サンプリングレートは入力サンプリングレートの4倍なので、補間係数Lは4である。