進化したオシロスコープを使いこなせる、 真のエンジニアになろう:いまさら聞けないオシロスコープ入門(1)(3/3 ページ)
立ち上がり時間は正確か?
波形がサイン波の場合を除いて、パルス波であれ台形波であれ、一番高速の変化をする部分に注目しなければなりません。最も高速に変化する部分に最も高い周波数成分が含まれているからです。正しい波形の表示(再現)には、一番高い周波数成分を再現できるかどうかがキーになります。例えば、周波数1kHzのパルス波形において、1kHzの周波数に注目する必要はほとんどありません。注目すべきなのは、最も高速に変化する、パルスの立ち上がり/立ち下がり部です。
さて、問題です。「立ち上がり時間1nsをうたうオシロスコープで立ち上がり時間1nsを持つパルス波を観測すると?」
答えは「立ち上がり時間は1nsより遅く見える」です。オシロスコープの立ち上がり時間の性能がパルス波形の立ち上がり時間に影響を与えるからです。約1GHzくらいまでのオシロスコープは高域減衰特性がガウス曲線に近似しており、この場合のオシロスコープの立ち上がり時間と被測定パルス波の立ち上がり時間との関係は次式で表されます。
例えば、1nsと1nsの組み合わせでは1.4nsくらいに見えます。約40%もの誤差になるわけです。
誤差を小さくするには
これをもっと小さな誤差で済ませるには、もっと速い立ち上がり時間を持つオシロスコープを使います。式に代入すれば、もっと誤差の小さな結果を得るために必要なオシロスコープの立ち上がり時間が分かります。「4倍の法則」があり、3%の誤差に収めるなら4倍高速のオシロスコープを使用すればよいことが分かります。
立ち上がり部が高速変化しており、0から1へ変化するのに1nsである場合を例に取ると、「4倍の法則」に従って、4倍高速の250psより速い立ち上がり時間をスペックしているオシロスコープを選択すればいいのです。
立ち上がり時間と周波数帯域を結ぶ定数、0.35
立ち上がり時間をスペックしていないオシロスコープの場合は、以下の計算式を適用することにより、周波数帯域から立ち上がり時間を計算できます。
<0.35 = 立ち上がり時間×周波数帯域>
この式により、上記の立ち上がり250psのオシロスコープは、1.4GHzの周波数帯域を持つオシロスコープであることが分かります。
真の立ち上がり時間が計算できる
オシロスコープの性能が高く、オシロスコープの立ち上がり時間Toが、測定される真値Tsより4倍以上高速なら画面に表示された測定値Tは誤差が少ないのですが、オシロスコープの性能がそれほど高くない場合、大きな誤差を含んだTが表示されてしまいます。
そこで前述のT = √(Ts2 + To2)により、真値Tsを計算により求める手法があります。つまりToが分かれば、画面に表示された測定値TからToの影響を除き、Tsを求めることができます。
問題です。オシロスコープの立ち上がり時間スペック値Toから計算したTsはどうなる?
答えは「真値より小さく計算される」です。オシロスコープの立ち上がり時間Toは必ず○○秒以下とスペックされています。つまり、オシロスコープの立ち上がり時間Toは「スペック値イコールではなく、本当はスペック値より小さい」です。よってオシロスコープの立ち上がり時間そのものを代入して計算すると、結果Tsは実際より小さめに計算されてしまいます。
言い換えると、真のTsは計算値よりちょっと大きめだと考える必要があります。可能なら、超高速パルスゼネレータを使用して測定した実際のオシロスコープの実力値Toを計算に用いれば、完ぺきです。2つ目の注意点は、Ts << Toでないこと。オシロスコープの性能があまりにも低く、Toが大き過ぎては、計算結果をToがほとんど支配することになり、Tsの不確かさが巨大になります。
Copyright © ITmedia, Inc. All Rights Reserved.
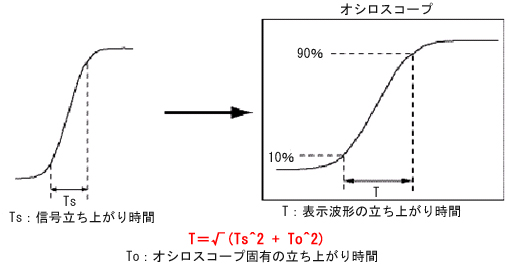 図6 オシロスコープ上の表示波形は「オシロスコープ固有の立ち上がり時間」の影響を受けている
図6 オシロスコープ上の表示波形は「オシロスコープ固有の立ち上がり時間」の影響を受けている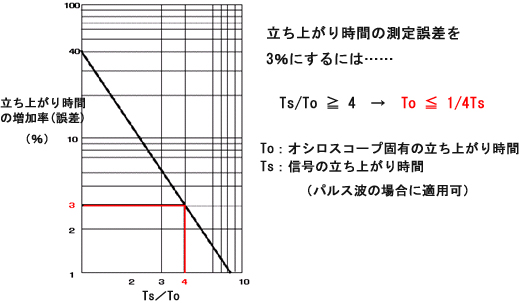 図7 入力信号とオシロスコープ固有の立ち上がり時間の関係
図7 入力信号とオシロスコープ固有の立ち上がり時間の関係



