サンプリング周波数変換でできる 効率的なFFT分析:イチから学ぶDSP基礎の基礎(6)(2/4 ページ)
デシメーションによるサンプリング周波数変換(周波数ダウン)
データの間引きを用いたサンプリング周波数変換システム(周波数ダウン)の一般化したブロック・ダイヤグラムは図7のようになります。
入出力のサンプリング周波数比はM:1となります。入力サンプリング周波数Fs-in=22050Hz、出力サンプリング周波数Fs-out=11025Hzの例ではM=2です。データの間引きの処理(図7のM↓)はデシメーションと呼びます。M:1のデシメーションはM個置きにデータを間引く操作になります。
サンプリング周波数ダウン
以下、サンプリング周波数前後の音声のスペクトログラム(いわゆる声紋表示)の例を示します。図の横軸は時間(秒)、縦軸は周波数(Hz)、色 は周波数成分の強さを表します(色が明るいほど強い)。
(1)サンプリング周波数変換前のファイルの一部のスペクトログラム(サンプリング周波数:22.05Hz)
(2)サンプリング周波数変換後のファイルの一部のスペクトログラム(サンプリング周波数:11.025kHz) デシメーションのみを行った場合。高周波成分の強いサ行の子音部分で折り返しひずみ成分がはっきりと分かる
(3)サンプリング周波数変換後のファイルの一部のスペクトログラムエリアジングを防ぐためのLPFを通した後でデシメーションを行った場合
横縞が見える部分は有声音(母音aiueo)。基本波と2次以上の高調波成分が縞模様に見えます。また、縞の間隔が音声の基本周波数となり、子音の部分は調波構造がはっきりとしないオレンジ〜赤色の塊に見えます。
周波数アップ
(その1)データはそのままでサンプリング周期を2分の1、サンプリング周波数を2倍にする処理(テープレコーダの早回し)
サンプリング周波数ダウンサンプリング周波数ダウンの次に、サンプリング周波数アップの方法を考えてみましょう。最も単純な例として、サンプリング周波数を2倍にするにはどうしたらいいかを調べてみます。まず、データに対する演算処理は施さずにサンプリング周期を2分の1にしたらどうなるか試してみましょう。
この処理では信号のスペクトルの形が変化してしまうために、信号処理を行うためのサンプリング周波数変換に使うことはできないことが分かります。
(その2)サンプリング周期を2分の1(サンプリング周波数2倍)にして、入力データを2サンプル分繰り返す処理
次に、サンプリング周期を2分の1にして入力データを2サンプル分繰り返してみるとどうなるか調べてみましょう。
このような処理でサンプリング周波数を1倍に上げた信号には、図11に示すようなひずみが生じます。
Copyright © ITmedia, Inc. All Rights Reserved.
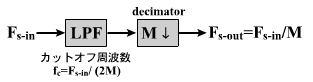 図7 デシメーションを用いたサンプリング周波数変換システム(周波数比Fs-in:Fs-out=M:1) Fs-in:入力サンプリング周波数、Fs-out:出力サンプリング周波数
図7 デシメーションを用いたサンプリング周波数変換システム(周波数比Fs-in:Fs-out=M:1) Fs-in:入力サンプリング周波数、Fs-out:出力サンプリング周波数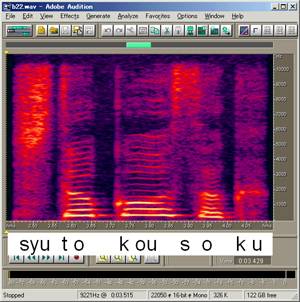
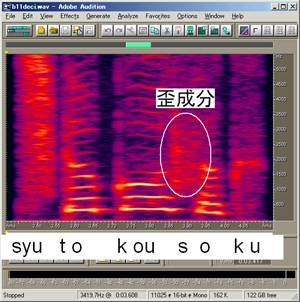
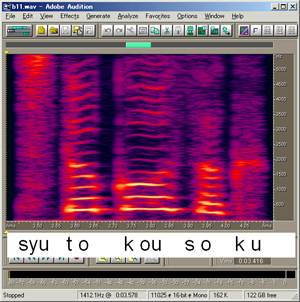
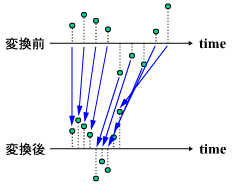 図8 データはそのままでサンプリング周期を2分の1、サンプリング周波数を2倍にした処理
図8 データはそのままでサンプリング周期を2分の1、サンプリング周波数を2倍にした処理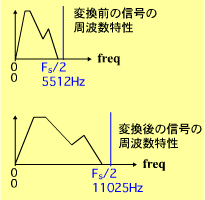 図9 変換前後の信号の周波数特性
図9 変換前後の信号の周波数特性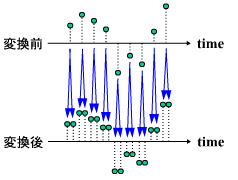 図10 変換前後の周波数
図10 変換前後の周波数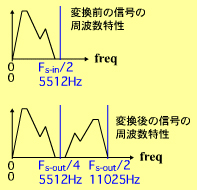 図11 信号のスペクトラムの変化 変換後の信号にはひずみが生じる
図11 信号のスペクトラムの変化 変換後の信号にはひずみが生じる


