CPUの中枢「ALU」を作ってみよう：マイコン入門!! 必携用語集（6）（3/4 ページ）

[菅井 賢，STマイクロエレクトロニクス]

減算器

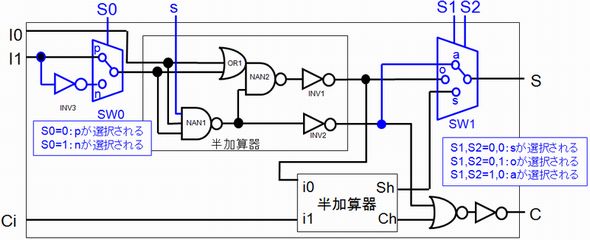
　マイコンの減算は、2の補数を加えて間接的に行います。加算器はできましたので、これに2の補数を作る回路を加えれば、減算器ができます。補数の作り方は、各桁を反転して、1を足せば出来上がります。先ほど作った加算器の入力信号の一方にインバータを付けて、その先に切り替え回路のスイッチを付けます。具体的には図8を見てください。

【図8】ALUの論理回路。青色の回路が追加回路を表す （クリックで拡大）

　SW0とSW1、信号線はS0〜S2、sが追加になっています。これらの追加回路の説明は順次行います。まず、SW0に着目してください。SW0がp側につながっているときはI1はそのまま加算器に入力されます。n側につながっているときI1は反転されます。これで各桁を反転することができます。I1を反転して、I0に1を入力して加算すると2の補数ができます。これをレジスタに保存しておいて、次の計算でこの2の補数を加えて、減算を行うことができます。

　実際のマイコンのALUでは、反転回路のところに、1を足す回路（インクリメンタ）が付いていて、1回で減算ができるようになっています。

　今回はALUの原理を学習するのが目的ですので、複雑にならないように、インクリメンタを付けない回路で説明しました。

AND回路

【図5】半加算器の論理回路

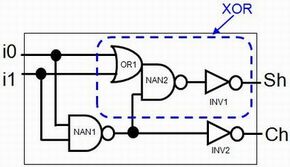
　次に論理演算を行いましょう。図5に示した半加算器の論理回路をもう一度、示します。じっと見てください。

　ANDとORが隠れているのが分かりますか？

　NAN1とINV2を組み合わせるとANDになります。OR1とNAN2とINV1を組み合わせるとORになります。しかし、このままではANDもORも使えません。ここからANDとORを取り出さなくてはなりません。そこで、先ほど説明した図8内の追加回路を使います。

　まずANDですが、NAN1とINV2の先をキャリーではなく、Sの方に出してやれば、I0とI1のANDが得られることになります。そこで、SW1を使います。ANDの演算を行いたいときにはSW1をaに切り替えます。するとSはNAND1とINV2で構成されるI0とI1のANDになることが分ります。ここで、sは1にしておきます。その場合、sはNAND1の出力値に影響は与えません。sはORを作る時に使います。

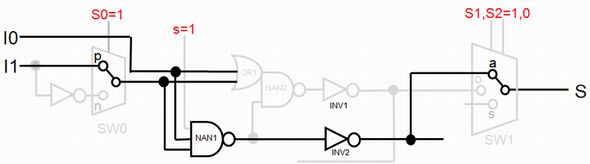
　図9を見てください。この図では、図8でAND回路を構成する要素だけ黒色にしてハイライトしましたので、分りやすいと思います。

【図9】ANDの論理回路 （クリックで拡大）

図9の解説

s=1, S0=0にすると、NAN1とINV2でANDになります。S0=0 , S1=1, S2=0にすると SW0でp、SW1でaのINV2を選択し、SはI0とI1のANDになります

　分ったところで、次にOR回路について考えましょう。