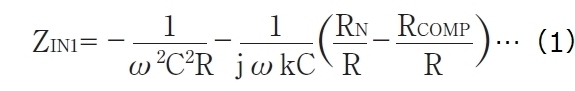振幅制御機能を備えたGIC発振回路：Design Ideas アナログ機能回路（1/2 ページ）

古典的なGIC（一般化インピーダンス変換器）に基づく回路である。固有の振幅安定化機能を備えた正弦波発振回路を紹介する。

[Lutz von Wangenheim（ドイツApplied Sciences 大学），EDN Japan]

一般化インピーダンス変換器（GIC）発振回路

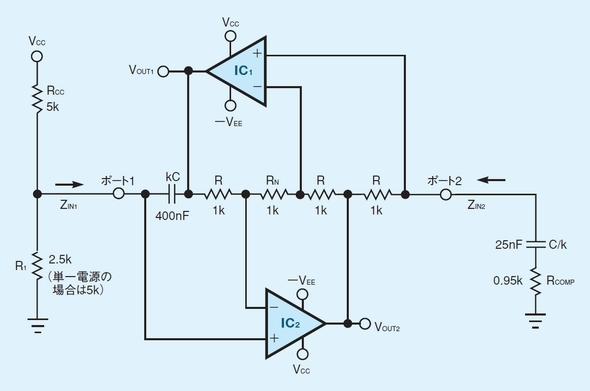
　図1は、古典的なGIC（一般化インピーダンス変換器）に基づく回路である。固有の振幅安定化機能を備えた正弦波発振回路だ。通常は2電源で動作する。ただし、抵抗R_CCを電源V_CCに接続すると単一電源電圧（V_EE＝0Vとする）で動かせる。

図1：GIC（一般化インピーダンス変換器）を利用した低ひずみの発振回路
振幅制御機能を備えた。

　発振周波数は、抵抗R₁を変えることによって調整できる。抵抗R_COMPは発振を安定化するために使用した。発振周波数とは関係しない。

　残りの受動部品は4個の同じ値の抵抗と、2個のコンデンサーである。コンデンサーの値はkCとC／kにする。ここでkはスケーリング・ファクターである。古典的なGIC回路と違い、この回路では抵抗R_Nを両オペアンプの反転入力の間に挿入している。

優れた高周波特性

　GIC回路は優れた高周波特性を有する。そのため、アクティブ・フィルター回路に広く用いられている。半導体インダクターやFDNR^＊1）素子を実現することもできる。

＊1）frequency-dependent negative resistanceの略で、周波数に依存する負性抵抗素子のこと。

　この回路の機能を説明する。まず、ポート1とポート2のGIC入力インピーダンスについて述べる。簡単な回路解析から、ポート1の入力インピーダンスとして次式が得られる。

　ここでR_COMP＝R_Nの場合は、式（1）は理想的なFDNR素子を表すことに注意されたい。このFDNR素子と、ポート1から接地へのシャント抵抗R₁とで、固有の発振能力を持った同調回路を形成する。しかし現実には、コンデンサーの損失と増幅器の不完全性による寄生効果のため、発振が止まってしまう。

　式（1）の第2項はR_COMP＜R_Nの場合に負性容量を示す。このことを利用して図1の回路では、損失を補償している。実際にはR_N＝Rとし、抵抗比R_COMP／Rは1より小さくて1に近い値に選ぶ（例えばR_COMP／R＝0.95〜0.98とする）。