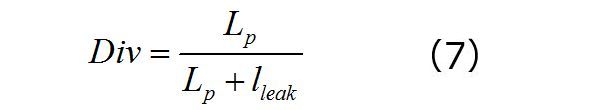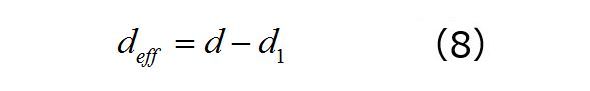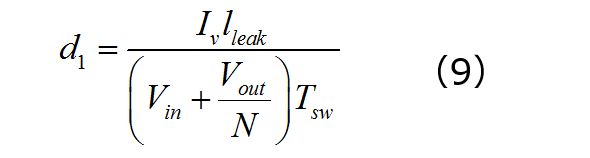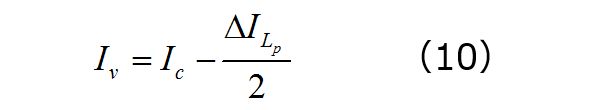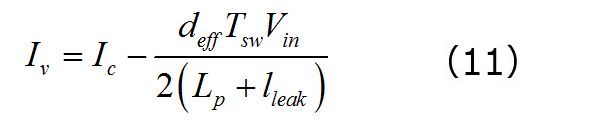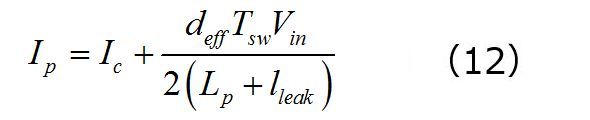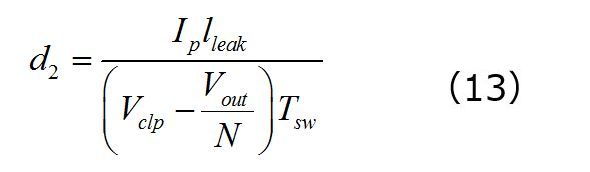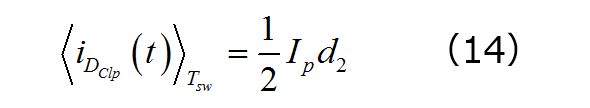漏れインダクタンスを使用したフライバックコンバーター（2） 平均モデル化：電源設計（3/4 ページ）

[Christophe Basso（ON Semiconductor France SAS），EDN]

漏れインダクタンスの考慮

　図5に示す平均モデルでは、モデルに印加されている電圧はV_inです。この電圧はdT_swの期間に1次側インダクタンスL_pをバイアスします。現実的には、第1回でみたように漏れインダクタンスを考慮すると、電圧は漏れインダクタンスと1次側インダクタンスの間で分割され、次のように電圧分割係数Divを形成します。

　このモデルに対する最初の変形は、V_inにV_in×Divを代入することです。2番目の変形には、デューティ比dが関係します。第1回では、デューティ比が漏れインダクタンス磁化時間d₁T_swに影響されることを確認しました。平均モデルに適用される実効デューティ比は、この事実を反映する必要があり、次式で表すことができます。

　d₁は漏れインダクタンス値（2次側ダイオード電圧降下V_fを無視）と谷点電流I_vに依存します。

　谷点電流を計算するために図7を再確認できます。谷点電流が実際は、平均電流I_cから1次側インダクタンスリップルの半分を引いた値であることが分かります。

　リップル電流は、L_pの直列接続に対してV_inを印加した結果生じた変位で、t_onつまりdT_swの期間におけるl_leakに相当します。したがって、谷点電流は次のようになります。

　ピーク電流は同様の方法で得られますが、上記のようにインダクタリップルの半分を減算するのではなく、I_cに対してインダクターのリップルの半分を加算する方法で求めます。

　クランピングネットワーク内を循環する電流は、漏れインダクタンスリセット時間d₂T_swにわたって持続します。もちろん、この時間はl_leakに依存しますが、反射されたV_outとクランプ電圧V_clpにも依存します。第1回から対応するデューティ比を次のように決定しました。

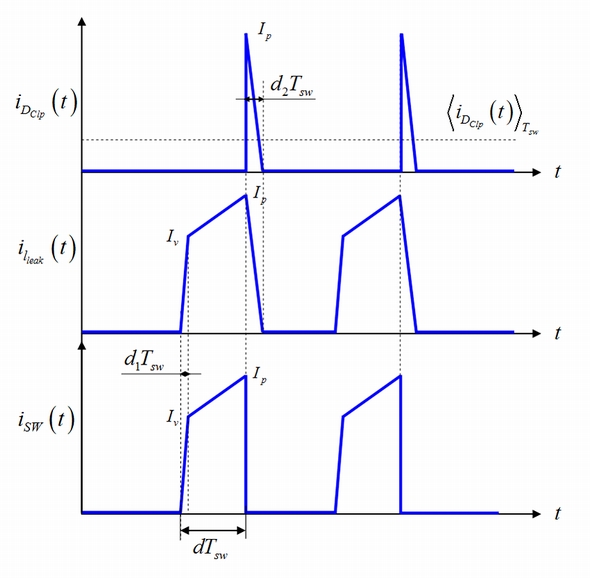
　図9はオン時間中にさまざまな電流が役割を演じることを示しています。下端はパワースイッチ電流で、それより上は漏れインダクタンスを流れる電流です。スイッチがターンオフすると、ほぼその直後に（C_lumpの充電時間を無視）電流はクランピングネットワークに流れを変え、急速にゼロに減少します。この時点で漏れインダクタンスはリセットされ、2次側電流はピークに達します。

図9：漏れインダクタンスのリセット時間d2Tswに電流はRCDネットワーク内を循環 （クリックで拡大）

　したがって、クランプダイオード内を循環する平均電流は単に、小さい三角形の面積をスイッチングサイクル全体で平均した値に等しくなります。