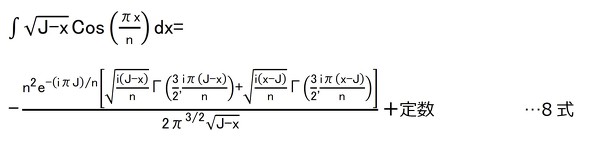ジャンクション温度の計算(4)―― 正弦波形損失の温度計算:中堅技術者に贈る電子部品“徹底”活用講座(78)(1/2 ページ)
今回はここまでの考え方に従って損失変化が直線ではなく正弦波で表される事例について検討を進めます。
» 2023年05月26日 11時00分 公開
[加藤博二(Sifoen),EDN Japan]
前回は任意の三角形の損失の温度上昇について説明しました。その結果同じピーク損失であっても三角形の形状によって温度上昇係数は0.471から0.667まで+40%近く変化し、波形の近似にはピーク損失だけではなく形状も重要になることが分かりました。
今回はここまでの考え方に従って損失変化が直線ではなく正弦波で表される事例について検討を進めます。
正弦波形損失の分解
図1のように最大損失P0、印加時間twの損失が正弦波的に変化する場合を考えます。
最初に正弦波損失Psを1式で定義します。
図2に示すようにこの正弦波損失の発生時間twをn等分(刻み時間Δt=tw/n)し、損失を刻みΔPiの矩形波に分割します。この損失の増加分ΔPiは1式を時間tで微分した2式を使って求めます。
2式のtは
ですから
を代入すると各時刻における損失の微少増加分ΔPiは3式で表せます(Δi=1)。
この正弦波損失について次のように計算を進めます。
この考え方を進めると第Jステップでは7式になります。
ここで手順としては7式を区分求積法と見なして積分を行い、区間0〜Jまでの定積分を求めたいのですが部分積分を施しても√項の次数が順次進んでいくだけでうまくキャンセルすることができません。
各種解法を試してみてもうまく解を得ることができず、数式処理ソフトの力を借りると8式の結果を得ることができました。
なお8式では簡略化のため、温度上昇係数のみを扱い、さらに数式処理ソフトがiを虚数と混用する可能性を避けるために変数をxとしてあります。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentPR
Pickup ContentsPR
Special SitePR
あなたにおすすめの記事PR
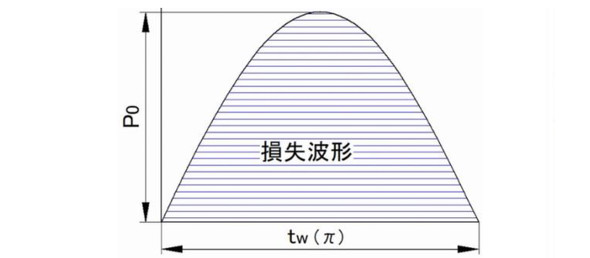 図1:正弦波損失の曲線例
図1:正弦波損失の曲線例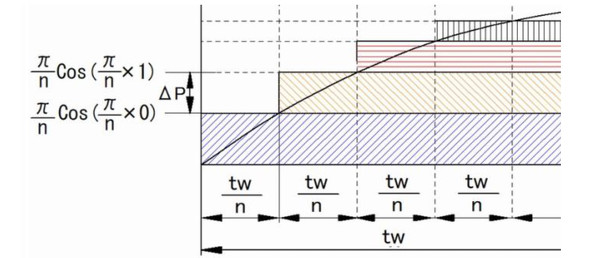 図2:正弦波損失の分解
図2:正弦波損失の分解
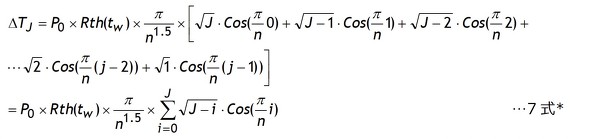 *7式は級数の最終項√(J-i)が0ですから実質的にはJ−1までと同じになります。
*7式は級数の最終項√(J-i)が0ですから実質的にはJ−1までと同じになります。