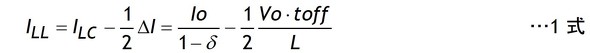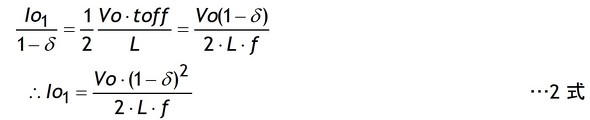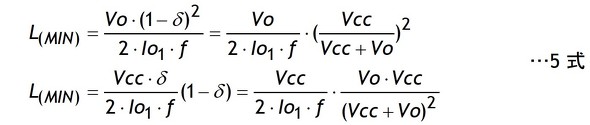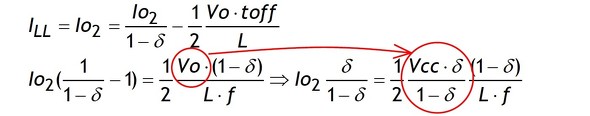反転形DC/DCコンバーターの設計(3)主要半導体部品の要求仕様:たった2つの式で始めるDC/DCコンバーターの設計(17)(2/3 ページ)
最小インダクタンス値LMIN
チョークを用いたDC/DCコンバーターでは負荷電流によって各部の動作が異なってきます。その影響を計算するために図1にチョーク電流ILと平滑キャパシターの電流波形を示します。平滑キャパシターへの充電電流は図1から分かるようにチョーク電流ILから負荷電流Ioを引いた(平行移動)波形になっています。
この計算で使用する記号は次の通りです。
IL:チョーク電流 ILP:ILのピーク値 ILL:ILの最小値
ILC:ILの中央値 Iin:入力電流DC値(ADC) Io:出力電流DC値(ADC)
Vcc:入力電圧(VDC) Vo:出力電圧(VDC) C1:平滑キャパシター容量
図1の各部波形について振る舞いを考えると次の6項目が分かります。
①ton期間中、ILはΔI=(Vcc/L)×tonだけ増加します。
②toff期間中、ILはΔI=(Vo/L)×toffだけ減少します。
③toff期間中のILはダイオードを通じて台形波状の電流となって負荷と平滑キャパシターC1に流れます。このチョーク電流ILの中央値ILCはIo/(1−δ)です。
④ILをIo分だけ並行移動した電流波形がC1充電電流の波形(◣部)です。
⑤C1充電電流波形の充電電荷(◣部面積)は放電電荷(■部面積)に等しくなります。
⑥toff終了時のILの状態(値)によって反転コンバーターは次の3つの動作状態に分かれます。
(1)toff終了時のILがIo以上であれば全toff期間でC1が充電されるMode I
(2)0A超、Io未満であればtc期間しか充電が行われないMode II
(3)0A以下であれば電流不連続モード
この条件から⑥の各値を計算します。
最初にILの最小値ILLを計算します。
1式のILLがIoになる負荷条件がMode IとIIの境界負荷電流値Io2であり、0Aになる条件がチョーク電流不連続モードになる臨界負荷電流値Io1です。まず電流不連続モードになる臨界負荷電流Io1を求めます。ILL=0ですから2式になります。
この2式に
を代入するとVccとIo1の関係を表す3式になります。
当然ですがこの臨界電流Io1は最小出力電流Io(MIN)より小さくなければなりません。
Io1を使って電流振幅ΔIを表すと次の4式になります。
参考:臨界インダクタンス値
チョーク電流ILが不連続になる臨界インダクタンスL(MIN)は2式や3式から逆算して求めます。
5式について詳しく説明しませんが臨界インダクタンスL(MIN)はVccが高いほど要求値が大きくなります。つまり同じL値であればVccが大きくなるほど不連続になりやすいことが分かります。
一方、Vccが一定でVoが変化した場合、L(MIN)の要求値はVcc>|Vo|の範囲で|Vo|に比例して大きくなり、Vcc<|Vo|の範囲では減少することが分かります。
次にMode I、IIの境界負荷電流値のIo2を求めます。手順はIo1と同様に1式においてIo=Io2とします。
この結果と3式から6式を得ます。
6式からIo2はIo1をδで除したものであること、つまり2つの電流値(Io1、Io2)はδで結ばれていて、お互いに無関係ではないことが分かります。
電流振幅ΔIをIo2で表す式は4式に6式を代入した7式になりますがIo2は仕様書には現れず、出力仕様との関連が弱いので実設計では7式よりも出力仕様と関連が強い4式を主に用います。
このΔIはコアのΔBに直結しているので仕様を満たすからといってIo1を大きくとると思わぬチョークの温度上昇を招くのでチョークの温度で問題を生じた時はこのIo1を見直すのも1手法です。
計算例
動作条件としてVo=−5V、Vcc=10V(δ=0.333)、L=55.5μH、f=100kHzを代入するとIo1、Io2として
が得られます。ですからIo=0.2〜0.6Aの範囲では平滑キャパシターC1の充電時間がtoff期間より短くなるMode IIになります。
Copyright © ITmedia, Inc. All Rights Reserved.
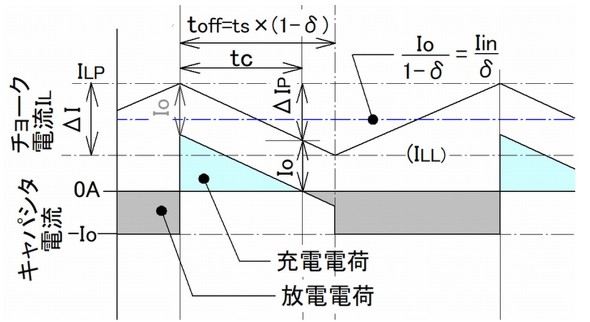 図1:代表的な動作電流波形例
図1:代表的な動作電流波形例