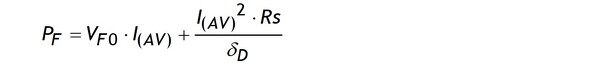反転形DC/DCコンバーターの設計(3)主要半導体部品の要求仕様:たった2つの式で始めるDC/DCコンバーターの設計(17)(1/3 ページ)
反転形DC/DCコンバーターで使用する主要部品の要求仕様について検討します。今回は入出力仕様からチョークの仕様を決めていきます。
前回は反転形DC/DCコンバーターで使用する主要半導体部品の要求仕様について検討しました。
ステップアップ形と同じディレーティングの考え方ですが動作原理が異なるので要求仕様についても微妙に異なってきます。今回は入出力仕様からチョークの仕様を決めていきます。
半導体への要求特性の比較
最初に前シリーズのステップアップ形コンバーターと今回の反転形コンバーターの要求特性の比較を表1に示します。両者ともオンオフ型のコンバーターですから同じ値のものもありますが回路構成の差に基づく差異もあります。
*:ダイオードのIF定格は順方向の損失PFに直結します。このPFはIF定格の他にもダイオードの通電率δDにも関係しますので次の手順でIF定格を選定します。ですが重要設計因子であるジャンクション温度TjはPFだけでは決まらずヒートシンクの熱抵抗Rthにも関係するので両者のバランスも重要です。
①最初にIo(MAX)の4倍程度のIF定格のダイオードを選定します。
②許容温度上昇ΔTj(=Tj(MAX)×0.8−Ta)とヒートシンクのRthから許容損失PF0(=ΔTj/Rth)を求めます。
③入出力条件からダイオード通電率δDを求めます。
④δDが決まればIF〜PF曲線を使って損失PFが①のPF0を満たすか判断します。
⑤δDパラメーターのPF曲線がない場合はDC損失曲線を次の近似式でδDをδD=1と考えてVF0とRsを求め、そのVF0とRsとδDを使って
の式で損失を見積ります。
⑥求めたPFとRthを使ってTjを計算し、結果が要求値と著しく懸け離れている場合はIF定格やRthを変更して②以後を再度実行します。
次に前回積み残したチョークL1の仕様について説明します。
チョークL1の要求特性
反転コンバーターの1回目で説明したように、チョークLに流れる電流ILは
で変化します。ここでIoは出力DC電流、δはFET(S1)の通電時比率、ΔIはチョークL1の電流リップル(=[Vo・(1−δ)]÷(2・L・f))です。この様子からチョークに必要な制約条件を考えます。
このΔIはインダクタンスの定義式(L×I=φ)からコアの損失パラメーターΔBに直結しています。したがって電気的仕様に問題がなくてもチョークのコア損失(温度上昇)の大きさからΔIは制限を受けます。
加えてこのΔIは後述するように最小負荷電流Io(MIN)も参考にして値を決めることになります。
飽和電流値I(SAT)の設定
前シリーズなどで既に説明したようにチョークのコアにはギャップ付きコアとノーギャップのコアがあります。
前者のギャップ付きコアのL-I特性は明確な飽和特性を示すのでI(SAT)の定義は明確であり、負荷短絡時などのチョーク電流ILのピーク値(=Io/(1−δ)+ΔI/2)の1.2倍以上のI(SAT)のコアを選定します。
このI(SAT)に対してマージンをとる考え方に対して「半導体の電流定格にマージンが取れればチョークに温度によるダメージが発生しない短時間ならチョークが飽和しても問題がないのではないか?」との考え方もあります。
ただしこの場合にはチョークの飽和特性が管理されていることが前提で、飽和特性がバラつく場合にはこの考え方には賛成できません。試作時に確認できても「量産での保証はどうするのか」を考えるとやはりチョークのI(SAT)の飽和を避ける観点からI(SAT)に対するマージンは必要です。
一方、コンポジット材などのノーギャップのコアには明確な飽和現象がありません。この場合には無重畳時のL値の70%になる重畳電流の値とメーカー定義の値とを比較して小さい方をI(SAT)とします。
最大負荷時のチョーク電流ILのピーク値は電流無重畳時のL値の80%に低下する重畳電流値やコイルの温度上昇などを参考に設定します。
明確な飽和ポイントがないコンポジット型のコア材の場合にはI(SAT)を超えたからといってL値が急激に低下するものではありません。
したがって一つの考え方ですが最大負荷電流時にチョーク電流のピーク値がI(SAT)以下であり、かつ温度上昇が規定値以内であれば熱的影響のない過渡時は半導体の電流定格を主体に判断することもあり得ます。
Copyright © ITmedia, Inc. All Rights Reserved.

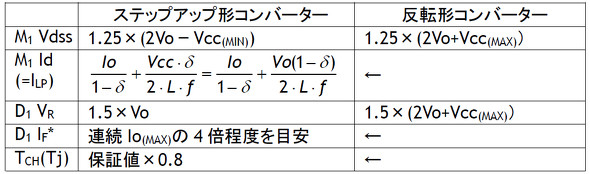 M1:SW用MOSFET D1:整流ダイオード Voは絶対値
M1:SW用MOSFET D1:整流ダイオード Voは絶対値