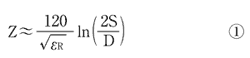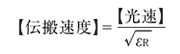ツイストペアケーブルのインピーダンス：Signal Integrity

[Howard Johnson，EDN]

　筆者は以前、ツイストペアケーブルのラインインピーダンスの近似式として以下の式を示したことがある。

　この式においてZは差動インピーダンス、ε_Rは比誘電率、Sは導体間隔、Dは導体直径である。

図1　ツイストペアケーブルの差動インピーダンスの計算例　図の条件の場合、差動インピーダンスの近似式における2S/Dの項は、2×1.3/0.95＝2.736となる。

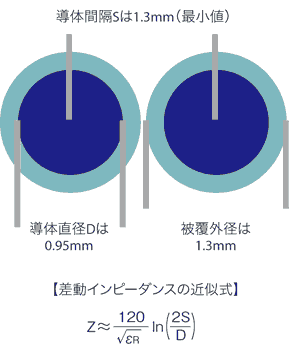
　この式に関して、つい最近、英Muirhead Aerospace社に勤務するOliver Kent氏から質問があった。その質問とは「私は外径が1.3mm、内径が0.95mmの被覆線材を使用している（図1）。被覆材としては比誘電率ε_Rの値が2のPTFE（Polytetrafluoroethylene）が用いられている。あなたの計算式にはln（2S/D）という項が含まれているが、この項は（導体間隔の2倍）÷（導体直径）が1以下の場合には負の値になる。この点の取り扱いについてご教授願いたい」というものだった。

　Kent氏は「導体間隔」を2本の線材の間の距離と理解したようである。しかし、これは筆者の定義とは異なる。筆者の式では、導体間隔を線材の中心から中心までの距離と定義している。従って、導体間隔は常に外径より大きく、それ故、2S/Dは常に2以上になる。すなわち、ln（2S/D）が負の値になることはない。

　ところで、式（1）はあくまでも近似式であり、完全なものではない。現実の使用条件では線材間がきつく押し付けられて導体間隔が狭くなることがある。そのような場合には、インピーダンスがゼロ近くまで低下することになる。このような条件は、式（1）では考慮していない。この式において、金属導体が互いに極めて近くにありS＝Dが成立すると、ln（2S/D）が最小の値ln（2）＝0.693となる。しかし、これは正しい結論ではない。

　式（1）は、導体間隔が十分に大きいことを前提として誘導したものである。この前提が成立する場合には、各導体の外周部に流れる電流は周に沿って均一に分布する。一方、導体が互いに近接している場合には、“近接効果”により、周に沿った電流分布が均一ではなくなり、かなりの電流が2本の導体間が向き合った面の部分に集中して流れる。式（1）では、このような近接効果は考慮していないので、導体が近接する場合のインピーダンスの計算値は高めの値となってしまうのである。

　インピーダンスが100Ωの通常のツイストペアケーブルでは、2S/Dの値はおよそ4になる。この場合、近接効果により生ずる電流分布の不均一はそれほど大きくない。実効抵抗値がわずか15％程度増加するくらいであり、インピーダンスへの影響もほとんど無視できる。この例に比べると、Kent氏が使っている線材の場合には、2S/Dがより小さいため近接効果はもっと顕著になる。

　式（1）については、考慮すべき点がもう1つある。それは実効比誘電率の概念に関することだ。

　導体周囲の電磁界の一部は誘電体層中にあるが、一部は空気層にも漏れ出す。そのため、実効比誘電率は空気の比誘電率（＝1）とPTFEの比誘電率（＝2）の中間の値になる。この値を正確に求めるには、2つに媒質に分布する電磁界エネルギーの相対比を計算に含めなければならない。

　2D電磁界解析システムが簡単に利用できるならば別だが、空気層と誘電体層にまたがる電磁界エネルギーの分布を求めるのは通常は困難である。そのため、式（1）に含まれる実効比誘電率が計算できないということになる。その場合には、対象とするケーブルにおける信号の伝搬速度を計測し、その結果から実効比誘電率を求める手法を使うとよい。伝搬速度と実効比誘電率の関係は次式で表せる。

　実効比誘電率が求まれば、その値を式（1）に代入してインピーダンスを概算することができる。

　ここで注意しておきたいのは、インピーダンスの変化は主に信号伝送系の寸法の変化によって生じるということである。線材の寸法が少し変化しても、実効比誘電率は大きくは変化しないからだ。

＜筆者紹介＞

Howard Johnson

Howard Johnson氏はSignal Consultingの学術博士。Oxford大学などで、デジタルエンジニアを対象にしたテクニカルワークショップを頻繁に開催している。ご意見は次のアドレスまで。www.sigcon.comまたは[e-mail]。