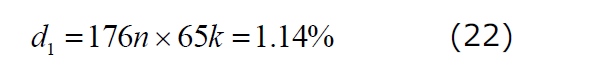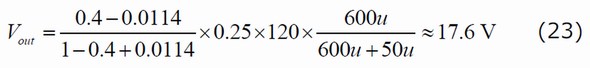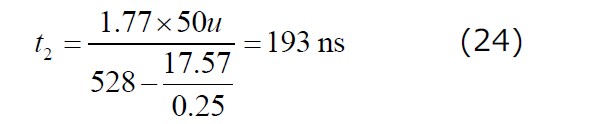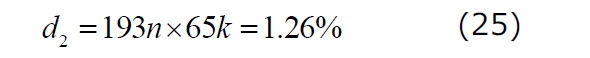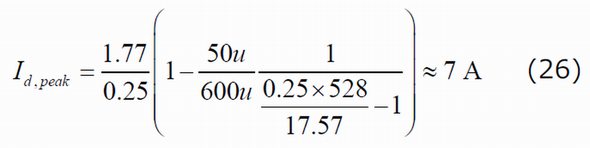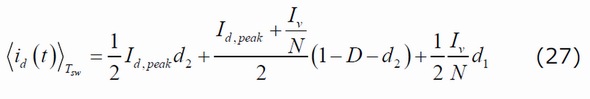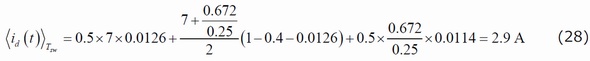漏れインダクタンスを使用したフライバックコンバーター（1）ハードウェア概要：電源設計（4/5 ページ）

[Christophe Basso（ON Semiconductor France SAS），EDN]

簡潔なサイクル単位モデル

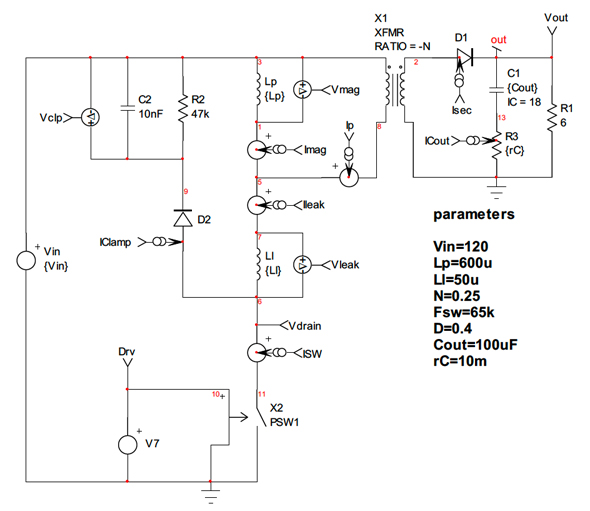
　上記の計算結果と波形を検証するために、40％のデューティ比で動作し、60Wをわずかに上回る電力を供給する簡潔なフライバックコンバーターをキャプチャーしました。電気回路図を図5に示します。漏れインダクタンスは50μHに設定されており、600μHの1次側インダクタンス（8.3％）を想定している場合は、疎結合のトランスを意味することになります。

図5：この簡潔モデルはフライバックコンバーターのシミュレーションに使用でき、基本的な波形を明示する （クリックで拡大）

図6：上記の全イベントを示す波形 （クリックで拡大）

　シミュレーションから、C₂両端の電圧がV_clpに等しい以下の動作ポイントを抽出できます。

I_p＝1.77A

I_v＝672mA

V_clp＝528V

　（14）で表記される漏れインダクタンス磁化時間について、176ナノ秒の測定結果が得られました。したがって、65kHzのスイッチング周波数を使用する場合、デューティ比d₁は次のようになります。

　理論的には、トランスの巻線比Nが0.25の場合、このフライバックコンバーターの出力電圧は、式（20）の定義に従って20Vに等しくなります。代わりに式（21）を適用する場合、出力電圧は、実際は次式に等しくなります。

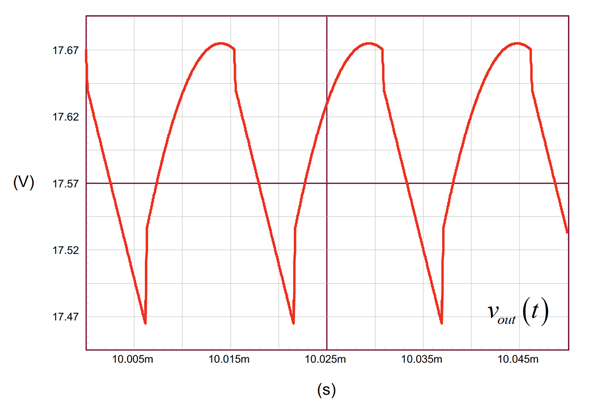
　シミュレーションの出力電圧は図7に示す通りであり、この値が正しいことを確認できます。シミュレーションで使用したダイオードの順方向電圧降下が0Vに等しいことに注意してください。ダイオード・モデルで拡散パラメーターNを10mに設定すると、この結果を得ることができます。

図7：上記の全イベントを示す波形 （クリックで拡大）

　漏れインダクタンスのリセット時間が分かれば、出力電流も高い精度で計算できます。シミュレーションの結果、672mAの谷電流および、672mAのピーク電流という値が得られました。式（16）を適用し、528Vのクランプ電圧（図5でC₂両端の電圧）を考慮すると、漏れインダクタンスのリセット時間は次式のようになります。

　また、この値は次のデューティ比に対応します。

　スイッチがオフになってから193ナノ秒後に漏れインダクタンスがリセットされた時点の2次側ピーク電流を推定することもできます。式（13）を適用すると、次の値が得られます。

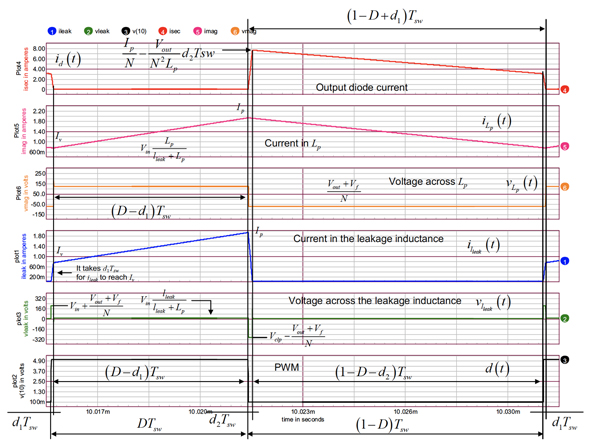
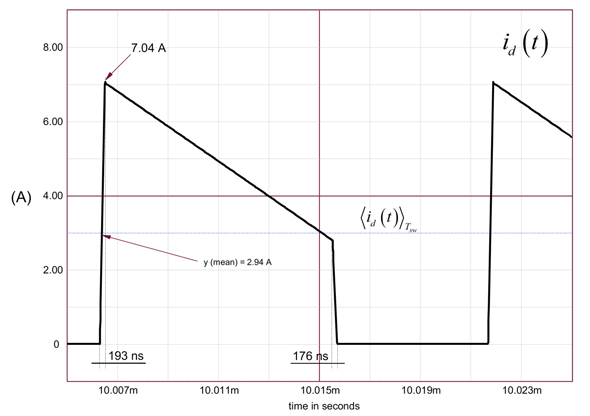
　図3の下側にある波形から、曲線を形成するさまざまな領域を計算することで、ダイオード内および負荷内を循環する平均電流を求めることができます。

　数値を代入すると、次のようになります。

　この値は図8に示す波形ビュワーで得られたものです。

図8：シミュレーションで得られる2次側平均電流はピーク電流およびさまざまな低デューティ比のd₁、d₂に依存 （クリックで拡大）