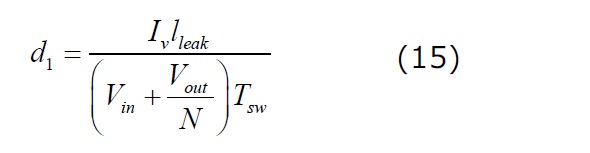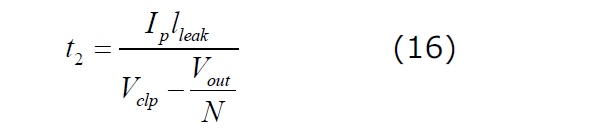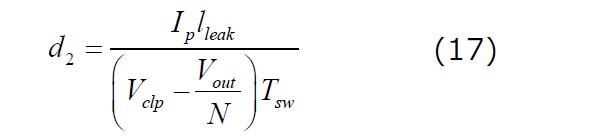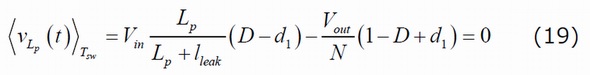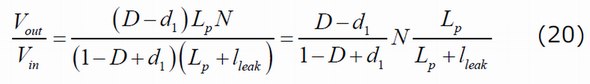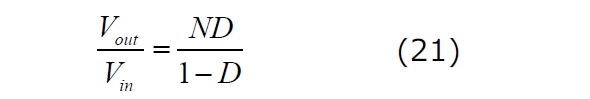漏れインダクタンスを使用したフライバックコンバーター(1)ハードウェア概要:電源設計(3/5 ページ)
DC伝達関数の更新
これまで、遷移時に発生している動作をより適切に理解することができました。ここで、上記の短時間イベントt1とt2を計算してみましょう。t1は0から谷電流Ivまで漏れインダクタンスがエネルギーを蓄積するのに必要な時間です。SWが閉じたときに、漏れインダクタンスの両端に印加されている電圧は、入力電圧Vinに対して直列となる反射出力電圧(ダイオードDは導通を継続)です。2次側ダイオードの順方向降下Vfを無視すると、t1は次のように定義できます。
スイッチング期間に対してこの時間を正規化すると、次式に等しいデューティ比d1が得られます。
漏れインダクタンスのリセット時間t2は、同様の方法で決定できます。スイッチが開いた時に漏れ要素の両端に印加される電圧は、(集中コンデンサーの充電時間を無視すると)、Dの導通が開始されているので、クランプレベルVclpから反射電圧を差し引いた値に等しくなります。それによって、次の値が得られます。
スイッチング期間に対して正規化を行うと、次式に等しいデューティ比d2が得られます。
コンバーターの出力電圧を決定するのに適したツールは、安定状態におけるインダクターLの両端の平均電圧がゼロであることを表すインダクターの電荷均衡則です。
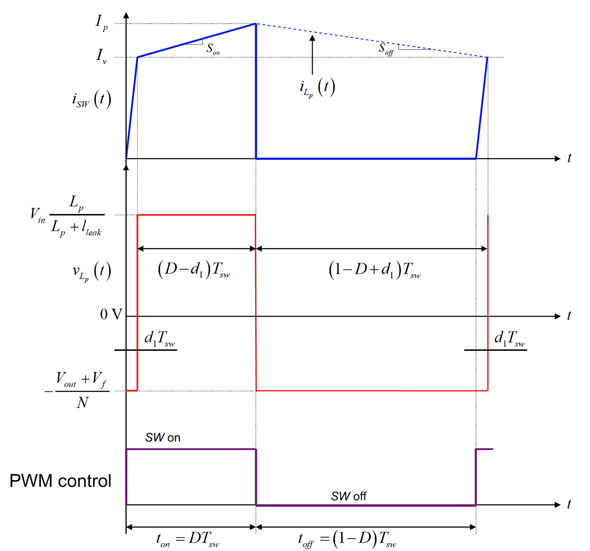
1次側インダクタンスの両端における電圧は、図4に示すグラフに従います。式(18)を満たすために、次式を記述することができます。
上式でVoutを求めて変形すると、次式が得られます。
これを簡略化すると、次のようになります。
ただし、この簡略化は、漏れインダクタンスがゼロの場合に成立する変形です。
興味深い点は、実効オン時間(つまり1次側インダクタンスの勾配が正である期間)が、実際のところDTswからd1TSWを引いた値に等しいことです。漏れインダクタンスが大きくなると、実効デューティ比はさらに小さくなります。また、1次側インダクタンスに印加される電圧もVinに等しいわけではなく、(1)で表記されている通り、それより小さい値です。
Copyright © ITmedia, Inc. All Rights Reserved.