アナログとデジタル帰還システムのループ安定性分析:DC-DCコンバーター活用講座(14) 帰還ループ(3)(1/3 ページ)
今回の記事では、アナログおよびデジタルループにおけるループ安定性の判定について解説します。
アナログループの安定性を実験に基づいて判定
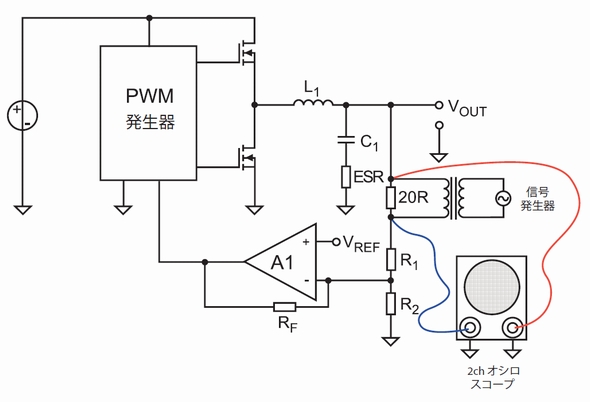
ボード線図装置を使って、実験に基づき帰還ループの安定性を判定することができます。正弦波発生器をオーディオ用トランスと併用して、制御ループに外乱信号を注入することができます。出力の外乱が外乱信号と同じ大きさになるまで、正弦波の周波数が徐々に増加します。ゲインはその結果1であり、外乱周波数はfC、すなわち帰還ループのコーナー周波数のはずです。外乱信号と出力の位相差が位相余裕です。さらに位相差が-180°になるまで周波数を上げることにより、ゲイン余裕を求めることができます。
ラプラス変換を使ってアナログループの安定性を評価
実験的手法に代わりに、ポールとゼロを数学的に導き出すことができます。この手法を実行するには、コンバーターの伝達関数が分かっていなければなりません。
連載第12回の図1に示された簡単な降圧コンバーターでは、伝達関数は次式のようになります。
文字「s」は、変数が周波数依存性を持つことを示します。伝達関数は、ラプラス変換(LT)を使って解くことができますが、LTを理解するには、まず、フーリエ変換について検討する必要があります。
フーリエ変換(FT)は特殊な形式のLTです。フーリエは、あらゆる周期信号は多様な周波数、位相、振幅の正弦波信号の和であることを突き止めました(フーリエ級数)。フーリエ変換は、時間領域から周波数領域へ変換を行います(逆もまた同じ)。周期信号に対するフーリエ変換の結果は、同等のフーリエ級数またはスペクトラムになります。図2に、矩形(くけい)波の最初の6つの高調波を図示します。
フーリエ関数は、負の無限大から正の無限大への積分関数で、次式で表すことができます。
S領域にマップすると、FTの変数はs=jωです。結果は虚の変数のみになります。
ラプラス変換はFTの上位に位置します。LTの変数は複素平面にあります。−∞ではなくゼロから積分が開始されます。つまり、ラプラス変換は、パルスや指数関数的に減衰する級数などの、ステップ信号や半無限大の信号を分析するのに使用することができます。ラプラス変換は次式で表すことができます。
S領域にマップすると、LTの変数はs=σ+jωです。
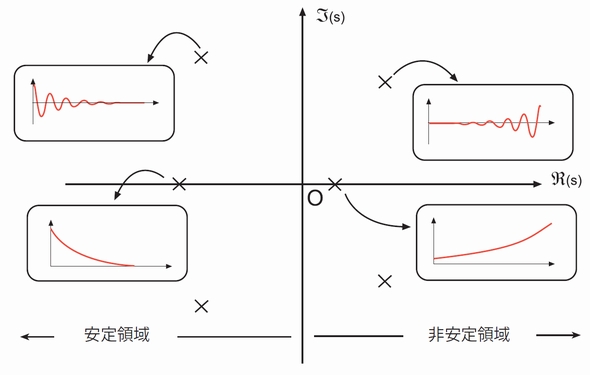
LTを使って、帰還ループを数学的にシミュレーションして、s平面にポールゼロプロットを生成することができます。縦軸は虚数で、横軸は実数です。虚数軸での上昇降下が大きいほど、高速の発振が起ります。負の実数軸で距離が離れれば減衰が速くなり、正の実数軸で離れると増加が速くなります。
ゼロは常に実数軸上にあります。s平面の左半分にある複素共役の1対のポールの組み合わせは、Ae−σtsin(ωt+φ)の形の減衰正弦波応答を生じます。ここで、Aとφは初期条件、σは減衰率、ωはラジアン/秒で表した周波数です。
虚数軸上にある(つまり、実数成分のない)1対のポール±jωは、一定の振幅の発振を生じます。
原点0からのポールの距離は応答がどれだけ減衰するかを表します。つまり、原点に近いほど減衰率は遅くなります。ポールが原点に位置すると、システムの動作はDCになります。
ポールが右半平面にあると、システムは不安定になります(これが、連載第12回で説明したRHP不安定性の語源です)。
Copyright © ITmedia, Inc. All Rights Reserved.
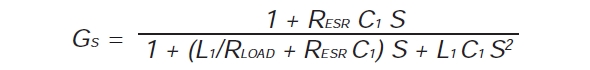 式1:連載第12回図1の伝達関数
式1:連載第12回図1の伝達関数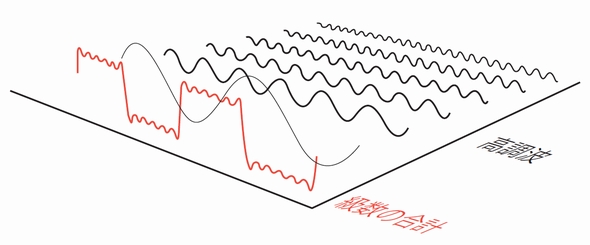
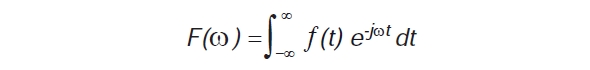 式2:フーリエ関数
式2:フーリエ関数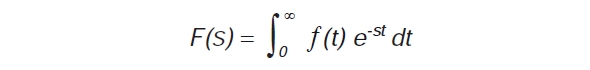 式3:ラプラス変換
式3:ラプラス変換