高速シリアル伝送におけるジッタの種類とその特長:高速シリアル伝送技術講座(10)(2/4 ページ)
特性の異なる2種類のジッタ 〜 RJとDJ
ランダムジッタ(RJ:Random Jitter)
ランダムジッタは図3左赤のヒストグラムのように富士山の裾野が広がるような形をしています。サンプル数が多くなると、青のヒストグラムのように裾野の広がりは大きくなり、トータルジッタ(TJ)は増加していきます。
サンプリング数に応じて裾野の広がりが変わるランダムジッタは、サーマルノイズやフリッカノイズなどの原因によって生じると考えられます。この左右均等に広がるヒストグラムは、自然界のばらつき現象に当てはまるガウス分布(正規分布)に近似すると確率統計学的に仮定して、標準偏差式1の平均値からのずれを示す係数σ(シグマ:二乗平均平方根)と、式2のσとμ(ミュー:平均)を使用したガウス分布に適応可能な標準偏差の確率密度関数(PDF:Probability Density Function)で表すことができると考えます。
式2でμ=0、σ2=1の場合、標準正規分布N(μ,σ2)の確率密度関数となります。これを±Xσまでの範囲を積分(実際は標準正規分布表、エクセルのNORM.DIST関数もしくは学術計算器を使用)し、全体に対する面積の比率(内側累積確率または内側累積比率と呼んでいます)を求めると、±1σ:68.26%、±2σ:95.44%、±3σ:99.73%、±4σ:99.994%、±5σ:99.99994%……となり、Xが大きくなればなるほど、全体の面積に対する比率は大きくなります。
表1は標準正規分布でXを変化させ内側積累比率を50桁まで表示したものですが、Xがいくら大きくても100%にはなりません。
このようにガウス分布で広がるランダムジッタの裾野の端はサンプリング数が多ければ多いほど無限に広がり、最大値を持ちません。ランダムジッタの値(最大値)を求めるためには、データシートに記載のランダムジッタ(RJ)のrms値(二乗平均平方根)や測定結果からのランダムジッタ成分のrms値を±1σとして、標準偏差の確率密度関数の積分で求められる内側累積比率(累積確率)が表2の必要なビットエラーレートから求めた比率(1−1/総ビット数)と等価なXの倍数値を使用します。一例ですが高品質が必要なデータ通信のアプリケーションでは、10-12のエラーレートを採用しています。
これが図4の中心μから左右に広がるランダムジッタの最大値(Peak to Peak)となります(ただし左右対称性のガウス分布にのみ適応)。
確定的ジッタ(DJ:Deterministic Jitter)
オシロスコープで波形を連続して上書し、ジッタのヒストグラムを表示すると図2左のように複数のピークが現れます。このピーク間の時間差が確定的ジッタ(DJ:デタミニステックジッタ)です。確定的ジッタ(DJ)はサンプル数にかかわらず最大値を持ち、Peak to Peakで表すことができます。
複数のピークの最も遠い2点間がDJの最大値になりますが、それぞれのピークにRJが伴って表示されます。よって、図2左のようにDJはサンプル数が多くなっても一定の値ですが、RJの裾野は広がるためトータルジッタは増加し、EYEの開口は小さくなります。
このRJとDJは、ジッタの階層構造を示す図5の2段目のジッタです。この2つのジッタを合わせると最上位のトータルジッタ(TJ)になります。
Copyright © ITmedia, Inc. All Rights Reserved.
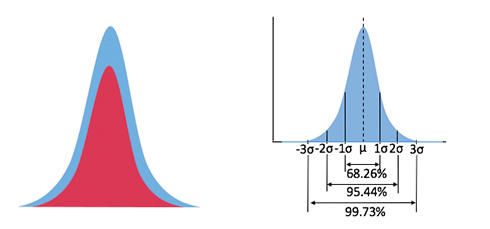 図3:左=サンプル数(赤:小、青:大) / 右=ガウス分布とσ(分散:シグマ)
図3:左=サンプル数(赤:小、青:大) / 右=ガウス分布とσ(分散:シグマ)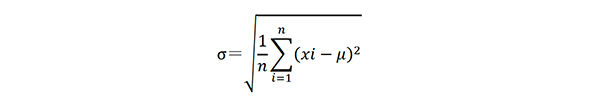 式1:標準偏差σ
式1:標準偏差σ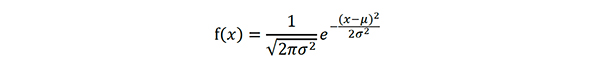 式2:ガウス分布の確率密度関数
式2:ガウス分布の確率密度関数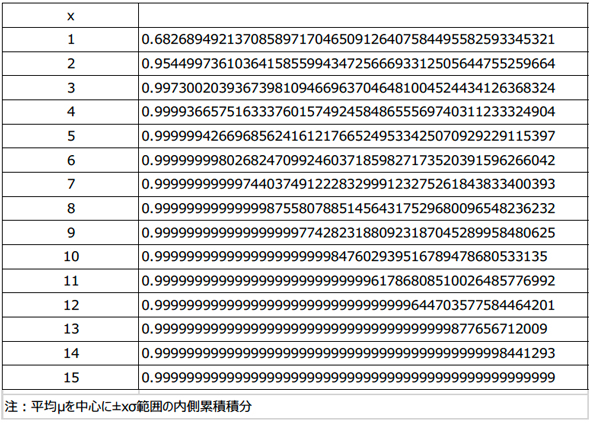 表1:標準正規分布 X=1〜15までの内積累積比率
表1:標準正規分布 X=1〜15までの内積累積比率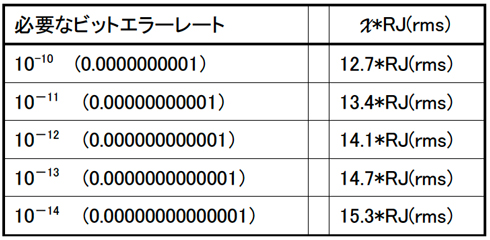 表2:ビットエラーレートとX,σの関係
表2:ビットエラーレートとX,σの関係 図4:エラーレート10-12時のランダムジッタ範囲
図4:エラーレート10-12時のランダムジッタ範囲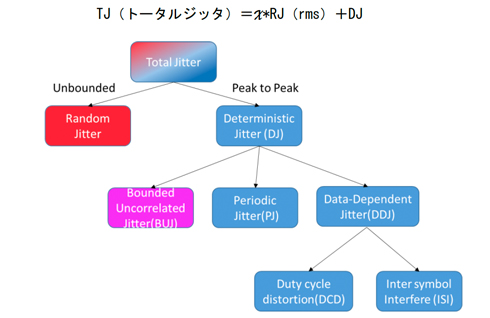 図5:ジッタの階層とその成分
図5:ジッタの階層とその成分


