電磁気学入門（6）コアレス〜近接効果：DC-DCコンバーター活用講座（49）（2/2 ページ）

[Steve Roberts（RECOM），EDN Japan]

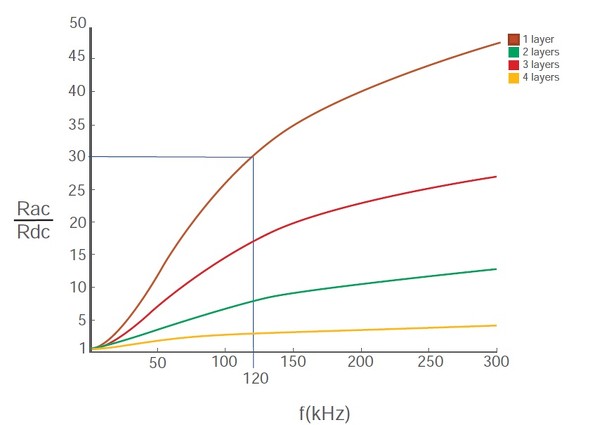
　近接効果による損失の計算は、1966年にP.L.Dowellが、周波数と層数に対するRac/Rdc曲線（図4）を導出するため、インダクターの層に関するマクスウェル方程式を解くための論説を書いた時に解決しました。彼の数学的解は改善がなされてきましたが、その本質部分は最初の有効な近似式として残っています。

図4：Dowellの周波数と層数に対する抵抗係数曲線

　120kHzで動作している一般的なDC-DCコンバーター（上図の青色線）では、近接効果は4層巻き線でAC抵抗をDC抵抗の30倍に増加させます。通常、多層巻き線では、近接効果による損失が表皮効果の損失を上回るのが容易に理解できます。

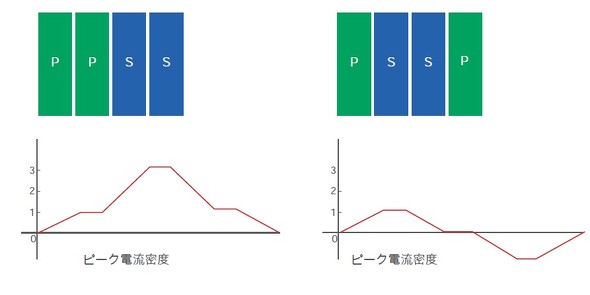
　トランスでの近接効果による電流集中は、巻き線を挟み込むことで低減可能です。単純な1：1、電流1A、一次側および二次側ともに2層のトランスを例に取ります。二次巻き線が単純に一次巻き線の上に巻かれた（一次−一次−二次−二次）場合、式11は、一次巻き線の最も外側の層と二次巻き線の最も内側の層に流れるピーク電流は、3Aになることを示しています。しかしながら、巻き線を一次−二次−二次−一次のようにした場合、巻き線間の近接効果は除去されるので、ピーク電流は公称電流である1Aになります。

　図5は、それを図式にしたものです。

図5：近接効果によるピーク電流密度と挟み込み効果

⇒「DC-DCコンバーター活用講座」連載バックナンバーはこちら

執筆者プロフィール

Steve Roberts

英国生まれ。ロンドンのブルネル大学（現在はウエスト・ロンドン大学）で物理・電子工学の学士（理学）号を取得後、University College Hospitalに勤務。その後、科学博物館で12年間インタラクティブ部門担当主任として勤務する間に、University College Londonで修士（理学）号を取得。オーストリアに渡って、RECOMのテクニカル・サポート・チームに加わり、カスタム・コンバーターの開発とお客様対応を担当。その後、オーストリア、グムンデンの新本社で、RECOM Groupのテクニカル・ディレクタに就任。

---

※本連載は、RECOMが発行した「DC/DC知識の本　ユーザーのための実用的ヒント」（2014年）を転載しています。