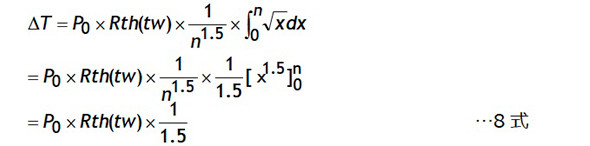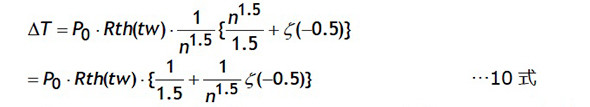ジャンクション温度の計算(2)―― 三角波状損失の温度計算の基礎:中堅技術者に贈る電子部品“徹底”活用講座(76)(1/2 ページ)
温度計算のツールともいえる原理(前提条件、仮定)を各種波形に適用し、得られた結果と従来の式を比較し、その妥当性を検討していきます。
前回は温度計算のツールともいえる原理(前提条件、仮定)について説明しました。今回からこの原理を各種波形に適用し、得られた結果と従来の式を比較し、その妥当性を検討していきます。
計算の途中で極限値を求めるためになじみのない式も使いますが数学が苦手な方は結論だけを読んでもらってもかまいません。メーカーのハンドブックなどの技術資料に記載されている値はこのような手順で導かれていると思ってください。
また一部の半導体メーカーが主張する過渡熱抵抗が極微時間域で45°モデルと相違する件はJEDECでは認めていないようです。
増加形三角波状損失の場合
本稿の温度計算では前回説明した
「重ね合わせの理」と
「45°熱拡散モデル{熱抵抗Rth(t)=R0・√(t)}」
を使用して計算を進めていきます。したがってチップの構造が異なる、パルス印加時間が長くなって熱抵抗が45°モデルから外れるなど前提条件が成立しないケースでは別途説明する計算法を使用する必要が出てきます。
ここで取り上げる損失波形として図1に示すような時間twの間、損失が時間に比例して最大損失P0まで増加する形状の場合を考えます。
この増加形三角波状損失を図2に示すようにn等分(刻み時間Δt=(tw)/n、損失刻みΔP=P0/n)して矩形波に分割します。
この三角波状損失について次のように1ステップずつ計算を進めます。
この考え方を順次進めると第Jステップでは4式になり、第(J+1)ステップでは5式になります。
次に温度上昇の最大値を調べるためにステップごとの温度上昇(ΔTJ+1−ΔTJ)を6式で計算します。級数の差分ですから最終項だけが残ります。
6式の各項は常に正ですから6式全体も常に正となります。したがってステップJが進行するにつれて温度が高くなることが分かります。
つまり増加形三角波状損失波形における最高温度は最終のt=twの時に発生します。この時の温度上昇ΔTは7式となりますが7式にはΣの項が含まれているのでn→∞では計算ができません。
ここで7式のΣ項を図3のように刻み幅1の区分求積法と考えるとΣ項は関数√(x)を0からnまで積分したものと考えることができます。
また、曲線より上の三角形の領域は分割数nを大きくすれば、つまり極限値である積分では相対的に0と見なせます。したがって7式の極限値は8式で表せます。
一方、7式を級数として解く手法ではnが大きい時のζ関数を使った近似式である9式を使用します。
7式のΣ項は9式にs=−0.5を代入したものですから7式は10式で近似できます。
10式のζ(−0.5)は有限値であり*、lim(n→∞)を考えると{ }内の第2項は0に漸近するので最終的な近似式は8式と同じ式になります。
Copyright © ITmedia, Inc. All Rights Reserved.

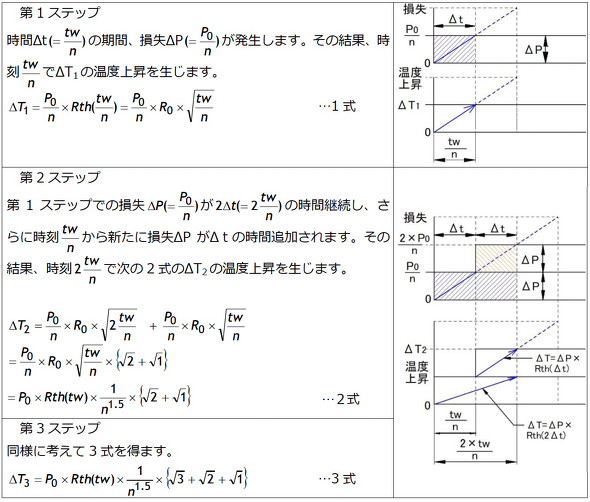
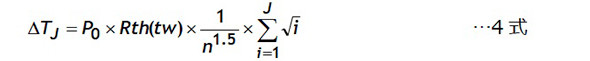
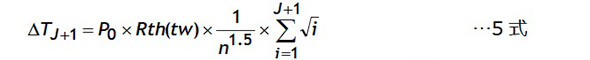
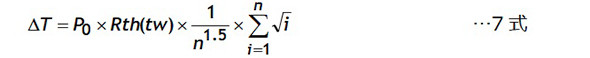
 図3:級数と積分
図3:級数と積分