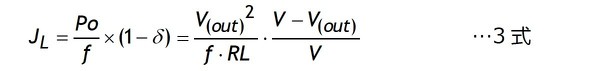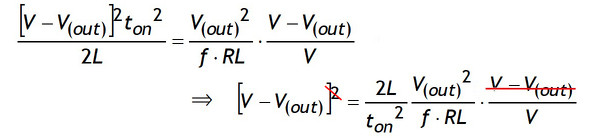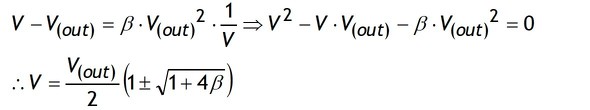ステップダウン形DC/DCコンバーターの設計（4）：たった2つの式で始めるDC/DCコンバーターの設計（6）（1/3 ページ）

[加藤博二（Sifoen），EDN Japan]

【連載一覧はこちら↑↑↑】

　前回は図式解法でリップル電圧を求めた結果、ステップダウン形DC/DCコンバーターの出力リップル電圧には負荷依存性はなく、入力電圧が高いほど大きくなることが分かりました。
　実機に湿式アルミ電解コンデンサーを用いた場合のリップル電圧は動作周波数が高くなるほどキャパシターのESRがリップル電圧を左右し、加えて1MHz動作ではコンバーター以外の実装上の要素も考慮しなければならないことも説明しました。
　今回はいままで前提にしてきたチョークの電流連続性が途切れた場合のコンバーターの振る舞いについて図式を基に検討します。このモードは「2つの式」だけでは説明が困難ですから「エネルギー保存則」を加えた2次方程式を通じて説明をしていきます。

電流不連続とは

　ここまではチョーク電流I_Lが瞬時でも0を下回らない前提で設計を進めてきましたが実際には半導体回路のラッチアップやファンモーターの停止などの負荷の異常やコネクター外れなどによる異常な軽負荷状態ではチョーク電流は1周期を通じて連続で流れることはできなくなります。
　ですが安全設計が要求される近年ではこの状態でもDC/DCコンバーターとして異常な状態にならないことを考慮して設計を進める必要があります。

　前述した軽負荷の場合には負荷抵抗はオン期間中にチョークに蓄積されたエネルギーをオフ期間中に消費できなくなり、余ったエネルギーで出力電圧は上昇します。その結果、オン期間中のインダクタンスの両端印加電圧V_Lは低下します。
　このV_Lの低下によってチョークLの蓄積エネルギーの増加は抑制されオフ期間の出力電圧はある電圧で安定します。
　また軽負荷ですから出力電流I_Oは減少し、既に説明してきたようにI_O＝ΔI/2を下回るとチョーク電流I_Lは底つきを起こして電流が連続して流れなくなります。
　このようにチョーク電流I_Lが1周期を通じて途切れてしまう区間を持つモードを電流不連続モードと呼びます（図1）。

チョーク電流不連続時の出力電圧

　注入されたエネルギーと負荷で消費されるエネルギーのバランスが成立する条件を考えます。「2つの式」と「エネルギー保存則」から導かれる2次方程式を解いているだけなので図と各式を見比べれば解析内容の理解は容易ですが「数式はチョット……」という方は4式まで読み飛ばしてもらっても構いません。
　時比率の計算が複雑になるのでここでは計算が簡便になる臨界モードで計算します。ですが“入ったエネルギーは必ず出ていく”というエネルギー収支は出力電圧V(out）に関係なく成立します。

図1：オン／オフモード別回路構成　（再掲）たった2つの式で始めるDC/DCコンバーターの設計（3）図2

　参考として連載第3回の図2「オン／オフモード別回路構成」を図1として再掲します。
　チョーク（インダクター）に蓄積される磁気エネルギーJ_Lは

で計算できることは既に説明しました。
　この式においてチョーク電流I_Lは両端に印加される電圧［V−V(out)］と印加時間tonとLの式（E･t＝L･I）から次のように計算できます。
　ここでV(out)はまだ決まっていません。

　1式をJ_Lの式に代入して1周期ごとに蓄積される磁気エネルギーJ_Lを求めます。

このエネルギーJ_LはスイッチS₁が遮断されるとエネルギー保存則に従ってV(out)としてエネルギー放出期間toff’中にキャパシターCに放出されます。したがってこのエネルギー（J_L）は平均化されてtoff期間の出力電力P_oになります。またton期間中の電力はチョークLを通じて電源Vから供給されます。
　1周期（1/f）のtoff期間中に消費されるこのエネルギーJ_Lは3式で計算できます（δ＝V(out)/V）。

　V(out)の様子を調べるために2式と3式を連立させ、まずVについて解きます。

　ここで

とすると

　負電圧は意味を成さないので“＋”の値のみを採用し、この式をV(out)について解きます。

　軽負荷時はRL→大ですからβ→小です。したがって4式からV(out)→大になり、最悪条件の無負荷時には出力電圧V(out)は電源電圧Vまで上昇することが分かります。

　このように電流不連続時には出力電圧V(out)が上昇するため、製品安全や負荷への損傷の範囲や程度などから過電圧保護回路は必要なのか？　必要なら検知レベルを何ボルトに設定するのか？ などの検討を行います。
　つまり負荷の異常時などでは出力電圧が何ボルトまで上昇するのかを事前に確認しておく必要があることになります。

注）前記の2式と3式を直接V(out)について解くと

を得ます。β＞0では得られる値は同じですがこの式ではβ＝0の時、0÷0となって値が定まりません。

図2：不連続時の各部電流波形