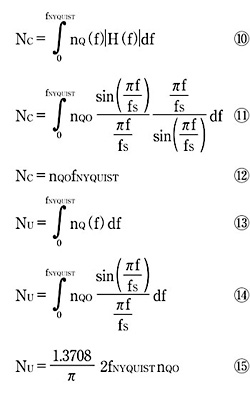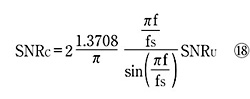D-Aコンバータの高域特性を改善する:高域特性劣化のメカニズムと3つの対応策(3/3 ページ)
【対策3】ポストイコライゼーションフィルタで補正する
アパーチャ効果の影響を回避するもう1つの方法は、周波数応答が逆sinc関数にほぼ等しいアナログフィルタを追加することである。このような「ポストイコライゼーションフィルタ」は、伝送線やアンプの補正によく使用されている。その手法を、アパーチャ効果の影響の削減に適用できる。
ポストイコライゼーションフィルタは、D-Aコンバータの再構成フィルタの後に挿入する。ここでは、簡単なアクティブフィルタを使用する例を示すことにしよう。
図7に示す例では、与えられた帯域幅に対して、ポストイコライゼーションフィルタの周波数応答がD-Aコンバータのsinc関数の周波数応答を打ち消すように、R1、R2およびC1の値を決定してある。この回路の場合、最大ゲインは1+R1/R2となる。周波数応答の平坦度を最適化する際には、SPICEシミュレーションを利用するとよいだろう。
典型的なポストイコライゼーションフィルタでは、ナイキスト周波数の50%以上まで−0.1dB以内の平坦度が保たれる。ポストイコライゼーションフィルタを使用しない場合、ナイキスト周波数の17%までしか−0.1dB以内の平坦度は得られないので、その効果は大きいといえよう。
補正しないD-Aコンバータのノイズが量子化ノイズのみであると仮定すると、アパーチャ効果により、出力信号とノイズの両方が減衰する。一方、ポストイコライゼーションフィルタを使用すると、高域になるほどノイズも増幅することになる。そのため、D-AコンバータのSN比にも影響が現れる。
補正済みのD-Aコンバータと補正を行わないD-Aコンバータの出力ノイズは、以下のようにDC付近からfNYQUISTまでのノイズパワーを積分することにより得られる。
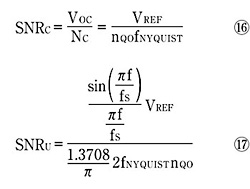
ここで、H(f)はポストイコライゼーションフィルタの周波数応答、nQ(f)はノイズパワー密度、nQOはDC付近の減衰していない量子化ノイズ密度、NCおよびNUは、それぞれ補正済みのD-Aコンバータおよび補正を行わないD-Aコンバータの総ノイズ電力である。最大SN比は基準電圧VREFで正規化されるので、補正済み、補正なしのD-AコンバータのSN比は、それぞれ以下のようになる。
また、以下のように両SN比の比をとることで、補正を行わない場合と補正を行った場合とで、SN比がどのように変化するのかを求めることができる。
この式から、補正済みD-Aコンバータの最大SN比は、低周波領域では劣化するものの、高周波領域においては向上することがわかる。
なお、ここまでの説明では、D-Aコンバータの再構成フィルタは理想的なローパスフィルタであると仮定し、その周波数特性はナイキスト周波数まで平坦で、その後急峻にゼロになるものとしている。しかし、実際の再構成フィルタの周波数特性は、カットオフ周波数近くでいくらか劣化する。プリイコライゼーションフィルタ、ポストイコライゼーションフィルタを用いる手法を採用した場合、この再構成フィルタの周波数特性の改善が行えるというメリットもある。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
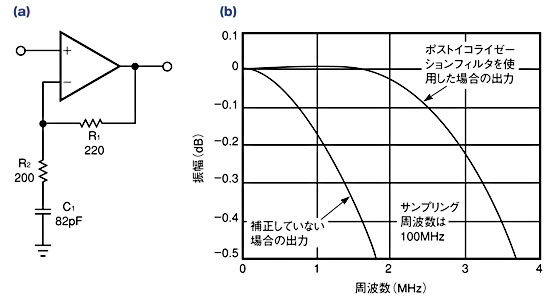 図7 簡単なアナログフィルタ(a)により、アパーチャ効果の影響を低減し、ナイキスト周波数の50%まで−0.1dB以内の平坦度を保つことができる(b)。
図7 簡単なアナログフィルタ(a)により、アパーチャ効果の影響を低減し、ナイキスト周波数の50%まで−0.1dB以内の平坦度を保つことができる(b)。