D-Aコンバータの高域特性を改善する:高域特性劣化のメカニズムと3つの対応策(1/3 ページ)
一般に、D-Aコンバータの周波数特性は、帯域内であっても平坦ではなく、高域に向かうほど減衰してしまう。本稿では、帯域内で平坦な特性を保つための3つの方法を紹介する。
D-Aコンバータの周波数特性を正しく把握して使用しているだろうか。一般に、D-Aコンバータの周波数特性は平坦ではない。帯域内(サンプリング周波数の1/2以下)であっても、高域側に行くに連れ、アナログ出力信号の振幅が減衰してしまう(図1)。例えば、サンプリング周波数をfSとすると、fS/2の80%の周波数信号では、出力振幅が2.42dBも減衰する。このことは、帯域内では平坦な周波数特性が必要となるアプリケーションでは問題となってしまう。
では、この問題を回避するにはどうすればよいのか。それには、以下に示すようないくつかの手法を用いることができる。
- 【対策1】サンプリング周波数を上げる
- 【対策2】プリイコライゼーションフィルタで補正する
- 【対策3】ポストイコライゼーションフィルタで補正する
以下では、これらの方法を順に紹介していくが、その前にまず「なぜ上述した問題が発生するのか」というところから押さえておこう。
D-Aコンバータの理想と現実
D-Aコンバータの周波数特性が平坦にならない理由を理解するには、まず最初に理想的なD-Aコンバータと現実のD-Aコンバータの違いを認識する必要がある。
図2をご覧いただきたい。これは、D-Aコンバータの出力を時間領域、周波数領域で表したものだ。理想的なD-Aコンバータの出力は、図2(a)のように、時間領域では電圧インパルス列となる。これを周波数領域で見ると、理想的なD-Aコンバータ出力が得られていることになる(図2(b))。
しかし、実際のD-Aコンバータの出力は図2(c)のような階段状の信号である。すなわち、ある出力電圧が更新レート(1/fS)の間だけ保持され、次の更新レートの開始時に次の出力電圧に切り替わる仕組みになっている。このような保持処理のことを「0次ホールド」と呼ぶ。この0次ホールドの影響により、実際のD-Aコンバータの出力を周波数領域で見ると、高域側の振幅が減衰してしまう(図2(d))。この現象を「アパーチャ効果(aperture effect)」と呼ぶ*1)。
アパーチャ効果により、D-Aコンバータの出力信号振幅は、理想的なD-Aコンバータ出力に、sin(x)/xを乗じたものとなる。このsin(x)/xという関数は、デジタル信号処理の世界では「sinc関数」としてよく知られている。sinc関数は、x=πf/fSとおくと、以下の式で表すことができる。
アパーチャ効果により、sinc関数の包絡線に沿って、主信号だけでなく、折り返し信号(イメージ信号)も大きく減衰する(図3)。この図からわかるように、アパーチャ効果の影響で、D-Aコンバータの出力ゲインはfS付近でゼロに近づく。同様に、2fS付近でもゼロに近づく。つまり、D-Aコンバータ出力の減衰パターンは、その更新レート(1/fS)に依存する。また、減衰量が−0.1dB以内に収まる範囲は約0.17fNYQUISTまでとなる。ここで、fNYQUIST=fS/2であり、この周波数を「ナイキスト周波数」と呼ぶ。
ここで、D-Aコンバータの基本を振り返ってみよう。
D-Aコンバータでは、入力信号が1つのインパルスであった場合、その出力は1/fS周期で更新されるパルス列となる(インパルス応答)。D-Aコンバータの周波数応答は、このインパルス応答をフーリエ変換することで得ることができる*2)。
帯域内のデジタル入力信号をD-A変換すると、それに対応する主信号のほかに、イメージ信号が現れる。1つ目のイメージ信号は、fS/2とfSの間に現れるが、fS以上の領域にも同様に繰り返し現れる。これらは通常、アナログローパスフィルタによって除去・減衰させなければならない。このローパスフィルタは、「再構成フィルタ(reconstruction filter)」とも呼ばれる。これはA-Dコンバータを使用する際に用いられる「アンチエイリアシングフィルタ」と対を成すものだともいえよう。
最初に現れるイメージ信号は、その周波数をfIMAGE、主信号の周波数をfOUTとすると、fIMAGE=fS−fOUTとなる。例えば、主信号の周波数fOUTが0.8fNYQUISTである場合、fIMAGE=1.2fNYQUISTとなり、それらの周波数の間には0.4fNYQUISTだけしか差がない状態となる。先述したように、イメージ信号は再構成フィルタで除去しなければならないわけだが、実際にはこのような条件でもイメージ信号を除去できるような再構成フィルタを実現するのは困難である。言い換えれば、D-Aコンバータで扱う最大信号周波数をナイキスト周波数よりも下に設定しなければ、現実的には再構成フィルタを設計することができない。一般的には、D-Aコンバータで扱う最大信号周波数は、ナイキスト周波数の80%程度に設定することが多い。
しかしながら、0.8fNYQUISTでは、アパーチャ効果により、出力信号振幅が実に2.42dBも減衰してしまう。この減衰量は、平坦な周波数応答を要するアプリケーションでは許容できない。例えば、減衰量が−0.1dB以内に収まっていなければならないとすると、この条件が満たされているのは、0.8fNYQUISTよりもさらに下の約0.17fNYQUISTまでである。この例であれば、振幅特性が平坦な周波数領域を0.8fNYQUISTまで広げるために、アパーチャ効果の影響を抑える方策が必要となるわけだ。
脚注
※1…Ifeachor, Emmanuel C and Barrie W Jervis, Digital Signal Processing: A Practical Approach, Second Edition, Addison-Wesley, 1993.
※2…Nilsson, James W and Susan Riedel, Electric Circuits, Fifth Edition, Addison-Wesley, 1996.
Copyright © ITmedia, Inc. All Rights Reserved.
 図1 D-Aコンバータの周波数応答は、高域になるほど減衰してしまう。
図1 D-Aコンバータの周波数応答は、高域になるほど減衰してしまう。  図2 理想的なD-Aコンバータでは、時間領域における出力は電圧インパルス列となる(a)。これを周波数領域で見ると(b)のようになる。しかし、実際のD-Aコンバータの出力は時間領域で見ると階段状であり(c)、これを周波数領域で見ると(d)のようになる。
図2 理想的なD-Aコンバータでは、時間領域における出力は電圧インパルス列となる(a)。これを周波数領域で見ると(b)のようになる。しかし、実際のD-Aコンバータの出力は時間領域で見ると階段状であり(c)、これを周波数領域で見ると(d)のようになる。 
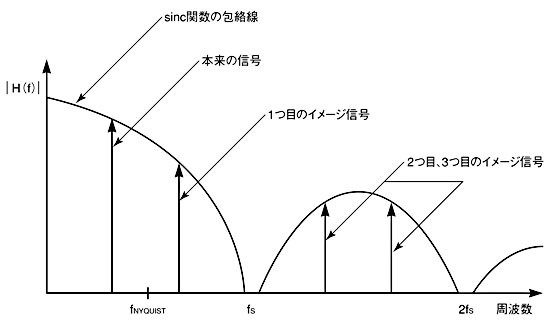 図3 D-Aコンバータの出力を周波数領域で表すと、本来の信号以外に、ナイキスト周波数以上の部分に多くの折り返し信号(イメージ信号)が発生する。イメージ信号も、アパーチャ効果によって減衰する。
図3 D-Aコンバータの出力を周波数領域で表すと、本来の信号以外に、ナイキスト周波数以上の部分に多くの折り返し信号(イメージ信号)が発生する。イメージ信号も、アパーチャ効果によって減衰する。 


