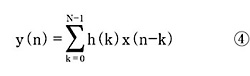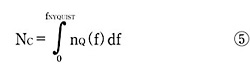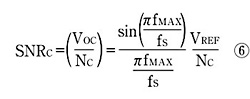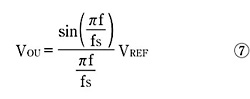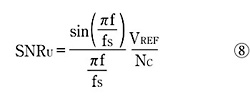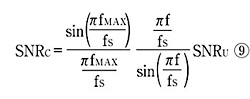D-Aコンバータの高域特性を改善する:高域特性劣化のメカニズムと3つの対応策(2/3 ページ)
【対策1】サンプリング周波数を上げる
それでは、アパーチャ効果の問題に対する1つ目の対策を紹介しよう。D-Aコンバータの出力信号の減衰は、その更新レート(サンプリング周波数)に依存する(図3)。そのため、入力信号の帯域幅は変更せず、単にサンプリング周波数を上げれば、アパーチャ効果の影響を最小限に抑えて帯域内の周波数特性を平坦に保つことができる。
D-Aコンバータのサンプリング周波数を上げることのメリットは、アパーチャ効果の影響を抑えられることだけではない。それ以外にも、量子化ノイズによって発生するノイズフロアーを低減し、再構成フィルタに対する要求を緩和できるというメリットもある。先ほども触れたように、再構成フィルタで厳しい要求を実現するのは困難であるため、このことも非常に大きなメリットとなる。
その一方で、サンプリング周波数を上げることには、以下のような問題点がある。
- 一般に高速なD-Aコンバータは高価であるため、コストが増大する
- 消費電力が大きくなる
- より高速なデータ処理が必要になる
こうした問題点はあるものの、上述したメリットを優先して、多くのメーカーはサンプリング周波数を上げる方法を採用している。ただし、単純にサンプリング周波数を上げるのではなく、多くの場合、以下で紹介する「補間手法」も併用するケースが多い。
ここでいう補間手法とは、D-Aコンバータの入力となる本来のサンプリングデータ列に、演算で求めたデータを挿入する処理のことだ。サンプルデータ列において、隣り合う2つのデータの間に、それらの間に存在するにふさわしいデータを新たに追加するのである。通常、この処理はデジタルフィルタを用いて実現する
例として、隣り合う2つのデータの間に1つのデータを挿入するデジタルフィルタを考えてみよう。この場合、総サンプルデータ数は元の2倍に増加する。これは、サンプリング周波数を2倍にしたのと等価的な処理だといえる。従って、D-Aコンバータは、2倍の速度で更新を行わなければならないことになる。
次に、8倍の補間を実現するために3つの補間段を持つデジタルフィルタを考えてみよう(隣り合う2つのサンプルデータの間に、合計7個のデータを追加する)。この場合、D-Aコンバータは、本来のサンプリング周波数の8倍の更新レートで変換を行わなければならない<*3)。しかし、この処理によって、アパーチャ効果によるsinc関数の周波数応答にも変化が起き、それがもう1つのメリットを生む。サンプリング周波数を上げない状態では、最初に出力ゲインがゼロになるのはfSのポイントだったが、サンプリング周波数を8倍に上げることにより、1つ目の減衰ポイントが8fSになり、平坦度が保たれる領域も8倍に広がる。これにより、再構成フィルタに対する要件がさらに軽減される。このメリットは非常に大きい。
なお、ここで紹介した方法は、ΔΣ変調や補間型デジタルフィルタを組み合わせて実現される「オーバーサンプリング型のD-Aコンバータ」でよく採用されている。つまり、オーバーサンプリング型のD-Aコンバータを使用している場合、アパーチャ効果はほとんど問題にならないであろう。
【対策2】プリイコライゼーションフィルタで補正する
上述したとおり、サンプリング周波数を上げると、アパーチャ効果の影響は軽減される。しかしながら、その影響を完全になくすことはできない。また、この方法の場合、D-Aコンバータを数倍高速に動作させることになる。従って、「D-Aコンバータの動作周波数はこれ以上、上げられない」という条件の下、アパーチャ効果の影響をさらに改善したければ、別の方法を選択せざるを得ない。
ここでは2つ目の対策として、周波数応答が逆sinc関数となるデジタルフィルタを使用する方法を紹介しよう。
逆sinc関数とは、1/sinc(x)で表される関数である。理論的には、そのようなフィルタを「プリイコライゼーションフィルタ」として用いれば、sinc周波数応答の影響を完全に打ち消し、完全に平坦な周波数応答を得ることができる。プリイコライゼーションフィルタは、デジタル入力データをフィルタリングし、D-Aコンバータにデータを送る前に高域の振幅を上げておくという役割を果たす。このようにすることで、アパーチャ効果の影響のない状態で元の信号を再現することが可能になる(図4)。
このデジタルフィルタの実現方法は任意だが、IIR(infinite impulse response:無限インパルス応答)型のものではなく、群遅延が発生せず、設計が比較的容易なFIR(finite impulse response filter:有限インパルス応答)型のものを用いるとよいだろう。
逆sinc関数を実現するFIRフィルタの設計には、周波数サンプリング手法(frequency-sampling techniques)を利用する。例えば、fS/2までの信号を扱いたい場合であれば、周波数応答H(f)におけるDCからfS/2までの間の値をサンプリングして求めればよい(図5)。次に、逆フーリエ変換によって、周波数サンプルポイントH(k)を時間領域におけるインパルス応答に変換する。インパルス応答係数は、以下に示すどちらかの式で表すことができる。
ここでH(k)(k=0, 1, ... N-1)は理想的な(あるいは目標とする)周波数応答を表す。また、h(n)(n=0, 1, ... N-1)は、時間領域におけるH(k)のインパルス応答の値であり、α=(N−1)/2である。正対称の線形位相FIRフィルタでNが偶数の場合、式(3)を用いてh(n)を単純化することができる。また、Nが奇数の場合には、総和の上限値は(N−1)/2となる*1)。
H(k)のサンプルポイント数(N)を増やすと、周波数応答は目標とするものに近づく。逆にH(k)のサンプルポイント数が少なすぎると、フィルタの効果が薄れてしまい、目標とする周波数応答から大きく外れてしまう。とはいえ、フィルタのサンプルポイント数が多すぎると、処理能力の高いデジタル回路が必要となってしまい、それもまた問題となる。最良な方法は、以下のようなものになるだろう。
(1)まずNとして大きな値を用いてh(n)を計算する
(2)得られた値の中から、いくつか数を絞ってh(n)を切り出す
(3)切り出したh(n)に窓関数(window function)を適用して平滑化する
ここでは、N=800としてh(n)を計算し、そこからh(n)を100点のみ切り出してブラックマン窓関数を適用した例を示すことにする。このようにして設計したFIRフィルタとD-Aコンバータを組み合わせた場合、ナイキスト周波数の約96%まで、−0.1dB以内の平坦度が保たれた周波数応答が得られる(図6)。補正を行っていないD-Aコンバータでは、−0.1dB以内の平坦度はナイキスト周波数のわずか17%までしか保たれないので、大きく改善していることになる。
インパルス応答を基に係数を得ると、以下のように、標準的なデジタル信号処理手法である畳み込み(convolution)によってFIRフィルタを実現することができる(x(n)は入力信号データ)。
なお、逆sinc関数を実現するフィルタは、高域上がりの周波数特性を持ち、その部分のゲインは1以上となる。従って、フィルタの出力振幅がD-Aコンバータの最大許容入力レベルを超えないように注意する必要がある。具体的には、問題が起きないレベルまで信号振幅を減衰させておかなければならない。入力信号の振幅を下げるため、sinc関数のフィルタを使用して補正を行う場合、補正を行わないD-Aコンバータよりもダイナミック特性が劣ることになる。
ここで、プリイコライゼーションフィルタによる補正を行う場合のSN比(信号対雑音比)の求め方を示しておこう。
一般に、出力ノイズは、DC付近から再構成フィルタのカットオフ周波数までのノイズパワー密度を積分することによって得られる。しかし、多くのD-Aコンバータメーカーは、以下のようにナイキスト周波数までのノイズを積分し、再構成フィルタを用いない状態でのSN比を求める方法を採用している。
この式において、NCはプリイコライゼーションフィルタによる補正済みのD-Aコンバータの総ノイズパワー(または電圧)である。また、nQ(f)はD-Aコンバータの出力ノイズ密度であり、この値は量子化ノイズと熱ノイズによって決まる。
補正済みのD-Aコンバータの最大SN比は一定で、周波数には依存しないが、以下のように最大出力周波数に依存する。
なお、式中のVREFは、D-Aコンバータの基準電圧、VOCは出力振幅を表す。
一方、補正を行わないD-Aコンバータの信号振幅は、sinc関数に沿って減衰した結果、以下のようになる。
補正を行わないD-Aコンバータのノイズパワーは、補正済みのD-Aコンバータのそれと同じである。従って、補正を行わないD-Aコンバータの最大SN比は以下のようになる。
また、補正済みのD-AコンバータのSN比の劣化分は、式(6)と(8)から得ることができる(以下参照)。
この式からわかるように、補正済みのD-AコンバータのSN比は周波数が低いほど劣化する。
脚注
※3…"MAX5895 data sheet," Maxim Integrated Products, www.maxim-ic.com.
Copyright © ITmedia, Inc. All Rights Reserved.
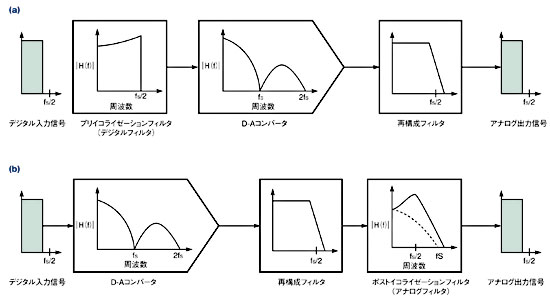 図4 プリイコライゼーションフィルタ(デジタルフィルタ)は、アパーチャ効果の影響を打ち消す(a)。ポストイコライゼーションフィルタ(アナログフィルタ)を用いても同様の効果を得ることができる(b)。
図4 プリイコライゼーションフィルタ(デジタルフィルタ)は、アパーチャ効果の影響を打ち消す(a)。ポストイコライゼーションフィルタ(アナログフィルタ)を用いても同様の効果を得ることができる(b)。 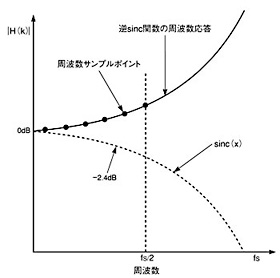 図5 逆sinc関数のDCからfS/2までの間のサンプリングを行うことにより、プリイコライゼーションフィルタの設計が可能。
図5 逆sinc関数のDCからfS/2までの間のサンプリングを行うことにより、プリイコライゼーションフィルタの設計が可能。 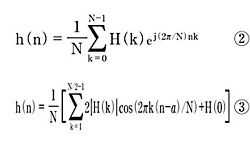
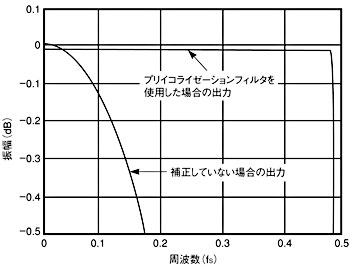 図6 FIRフィルタにより、D-Aコンバータの周波数特性が改善され、ナイキスト周波数付近まで−0.1dB以内の平坦度が保たれる。
図6 FIRフィルタにより、D-Aコンバータの周波数特性が改善され、ナイキスト周波数付近まで−0.1dB以内の平坦度が保たれる。