FPGAで作る任意波形発生器(2/4 ページ)
回路の基本構成
周波数fの信号を発生する回路は、例えば24ビットの位相アキュムレータを水晶発振器からの20MHzのクロックで駆動する構成によって実現できる。この構成を用いて、例えば周波数が501.1Hzの出力信号を得ようとする場合、必要なΔNは式(7)によって以下のように計算できる。
すなわち、24ビットの位相アキュムレータは、入力クロックの1パルス当たり420だけカウントアップする。カウンタは、最大値である2kを超えたときにはカウント値を0に戻す。位相アキュムレータのMSB(most significant bit)の変化が出力周波数に相当することになる。
図1は任意周波数発生器の基本構成例を表している。この例では、マイクロコントローラにFPGAを接続する構成としている。この場合、マイクロコントローラが式(8)に示したΔNをカウントし、その結果をFPGAに対して8ビットのデータバス、2ビットのアドレスバス、書き込み(wr)制御信号を利用して送出する。位相アキュムレータはMSBを出力とするので、ΔNの値は(k−1)ビットで表現できる。言い換えれば、ΔNは2k−1を超えることはないということである。
リスト1は、FPGAの詳細動作を記述したVerilog HDLコードである。この回路の動作を以下の2つの具体例で説明しよう。
1つ目の例は、20MHzのクロックを基に、10MHzの出力周波数を生成するというものである。この場合のΔNは式(7)から、224/2、すなわち838万8608となる。このΔNに対する回路の動作、すなわち1クロックごとの位相アキュムレータのカウント値と任意周波数発生器の出力に相当するMSBの値の関係を表1に示す。表からわかるように、この例は単純な2分周相当のものとなる。
もう1つの例として、9.999998808MHzの出力周波数を生成するケースを考える。この場合、式(7)で計算したΔNは838万8607、すなわち1つ目の例のΔNより1だけ小さい値になる。表2に、224個のクロックに対する位相アキュムレータのカウント値とMSBの値を示す。表の赤字表記の個所はMSBの値が変化していないところであり、これから0→1の遷移と1→0の遷移がそれぞれ1回ずつ抜けていることがわかる。この例の出力周波数は10MHzより1.192Hzだけ低い値になる。
Copyright © ITmedia, Inc. All Rights Reserved.
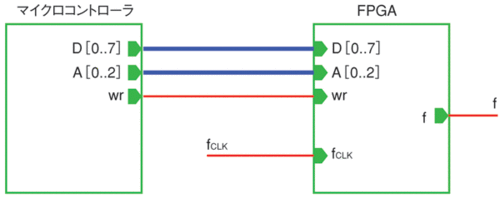 図1 任意周波数発生器の基本構成
図1 任意周波数発生器の基本構成  リスト1 FPGA用のVerilogHDLコード
リスト1 FPGA用のVerilogHDLコード 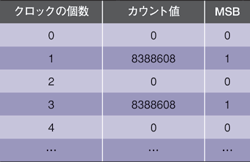 表1 位相アキュムレータのカウント値とMSBの値(その1)
表1 位相アキュムレータのカウント値とMSBの値(その1) 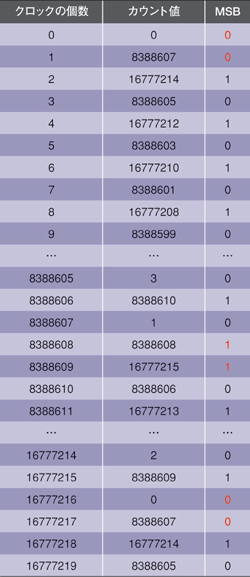 表2 位相アキュムレータのカウント値とMSBの値(その2)
表2 位相アキュムレータのカウント値とMSBの値(その2) 


