FPGAで作る任意波形発生器（3/4 ページ）

[Eugene Palatnik（フランスITEC Engineering社），EDN]

分解能とダイナミックレンジ

　続いて、出力周波数の分解能はどうなるのか考えてみる。すなわち、所望の周波数にどこまで一致させられるのかということだ。

　まず、2種類のカウント値ΔN₁とΔN₂を考える。これらの値によって、2種類の周波数f₁とf₂が次の2つの式のように決定される。

　ΔN₁とΔN₂の値の差は最小で1である。この差に対応するf₁とf₂の差は上の2つの式から次のように計算できる。

　これは以下のように変形できる。

　これらの式から、周波数の分解能は、入力クロックの周波数と位相アキュムレータのビット長によって決まることがわかる。

　それでは、周波数のダイナミックレンジ（周波数が変化する範囲）はどうなるだろうか。これについては、ΔNが取り得る値の範囲、すなわち1から2^k−1の範囲がダイナミックレンジを決める。

　以上をまとめると、上に挙げた例で言えば、0.596Hzから10MHzまでの範囲の周波数を分解能0.596Hzで生成できるということである。

任意波形の生成

　ここまでで、任意の周波数（クロック）を得る方法はわかった。続いては、これを利用して、任意の波形を生成する方法について考えてみる。ここでは、心電図（ECG：electrocardiogram）シミュレーションに用いるような任意周波数発生器を例にとる。

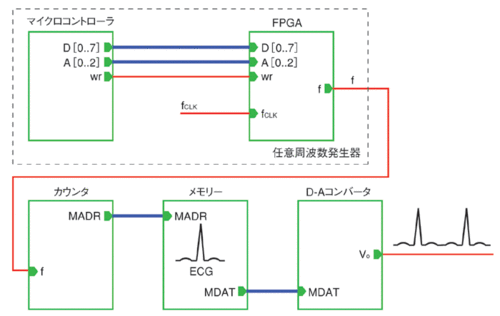
　図2に示したのが、図1の任意周波数発生器を利用して構成した任意波形発生器である。このシステムでは、生成すべき目標波形の1周期分のデータをメモリーに格納しておく。この状態で、任意周波数発生器からのサンプリングクロックによって循環カウンタ（circular counter）が動作し、その出力によってメモリーアドレスが呼び出される。その結果、メモリーから各クロックごとに新しいデータがD-Aコンバータに送られ、アナログ出力電圧が更新されることで任意波形を得る仕組みである。

図2　任意波形発生器の基本構成