Spiceの新しい応用解析:自然対流問題(その2):SPICEの仕組みとその活用設計(20)(1/3 ページ)
CFDツールでなければ解けない自然対流問題に適用できる熱抵抗回路網法ですが、単にSpice回路網上で実現させてもうまく動作しません。今回はいかに動作させるか、そして完成した回路の精度と妥当性について検証を行います。
前回説明した熱伝導率λと熱伝達係数Hの違いは覚えているでしょうか。前回はCFDツールでなければ解けない自然対流問題に適用できる熱抵抗回路網法を紹介するとともに、その解法をSpice回路網上で実現させたところ、うまく動作しない課題が残ったところまでを紹介しました。この時点で多くの方は「何だ、やはりダメなのか?」と思われたかもしれません。
事実、Spiceセミナーで採り上げられる熱問題が固体内の熱伝導に限定されているのはそのような課題が含まれているからなのですが、今回はその回路をいかに動作させるか、そして完成した回路の精度と妥当性について検証を行います。
Spiceへの実装
まず、前回提案した熱抵抗回路網法のイメージ回路を図1に再掲します。
前回説明した通り、図1の電圧制御型の可変抵抗で熱伝達係数を表現することは困難であるということが分かってきましたので何か別の次元の方法でSpiceへの実装を考える必要があります。
ここで、本連載の第3回で説明したようにSpiceは半導体回路を主とした非線形回路網を解くのが本来の機能であるということを思い出してください。
普段、特に意識して設定はしていませんがSpiceにはこのような変数を含んだ回路網を解く機能があります。解法アルゴリズムはニュートン・ラフソン法で、電圧を計算→コンダクタンスを計算→電圧を再計算→コンダクタンスを再計算→電圧を再計算……を繰り返し行い収束させていきます。
では、今回の場合ではこの自動収束の機能をどう当てはめていけば良いのでしょうか?
前回、表1のように熱流量は電流に、温度、温度差はそれぞれ電圧、電位差に置き換えられることを述べ、熱伝達係数Hc、Hrは次の1、2式に示すように温度に関係していることを述べました。
また、対流熱伝達係数Hcの各パラメータは面の方向によって表2のように決められていることも併せて述べました。
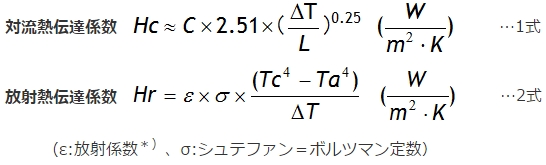 *)放射係数ε:表面の状態によって0〜1の値をとる係数です。理想黒体放射の場合はε=1、完全反射状態の場合はε=0の値をとります。赤外線温度計で表面温度を実測する場合はεを正しく設定しないと誤差を生じます。
*)放射係数ε:表面の状態によって0〜1の値をとる係数です。理想黒体放射の場合はε=1、完全反射状態の場合はε=0の値をとります。赤外線温度計で表面温度を実測する場合はεを正しく設定しないと誤差を生じます。基本的には表面の色が支配し、表面処理の状態は影響しません。ただし、非常に塗膜が厚く、1つの部材として熱伝導の影響を考慮しなければならない場合は除きます。
これら1、2式を見てみると、熱伝達係数Hの単位[W/(m2・K)]に面積と温度差を掛けてやればWの単位、すなわち電流の単位になることが分かります。つまり対流熱伝達Hcの場合であれば、図2に示すように温度差ΔTに対応して、
となる電流が流せれば良いわけです。
(ΔT:固体表面温度Tcと流体の温度差)
表1に記したように温度は電圧に対応していますので、Spiceにおいて高次関数を記述でき、なおかつ電圧で電流を制御できるデバイスがあれば可能性が出てきます。
これらを満たすSpiceで置き換えられそうなデバイスを探すと、非線形電流源が見つかりました。いわゆる"Bデバイス"で、PSpiceではBデバイスが見つかりませんでしたので"ABM/Iデバイス"を使用します。
これらのデバイスは図2に示すように回路中の制御電圧によって流れる電流が制御され、収束判定はSpiceの非線形解析機能が受け持ってくれるため、設計者が繰り返し計算の設定を気にする必要はありません。
放射熱伝達係数Hrについても対流熱伝達係数Hcと同様に考えれば良く、4式や図3のようになります。
これらHc、Hrを表す非線形電流源を物体(固体)の各面に設置すれば良いわけです。総合の等価回路を図4に示します。
ただし、図4では計算間違いを防止する意味と理解のために対流熱伝達係数Hcは上面、下面、前後面、左右面に分けてBデバイスを4個設け、放射熱伝達係数Hrを表すBデバイスを1個設けてあります。
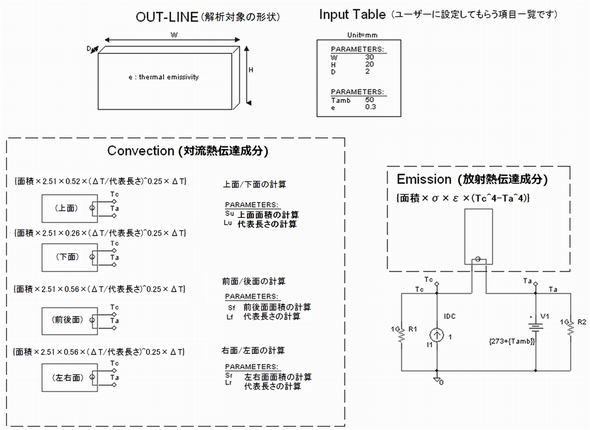 図4 熱抵抗回路網の計算等価回路
図4 熱抵抗回路網の計算等価回路注1:図4中のR1、R2はフローティング対策用の抵抗です。値は1GΩなので400K前後の計算には影響しません。
注2:TcとTaの接続は回路図を簡素化するために接続端子による回路図内Jumpとしてあります。
熱伝達係数Hには前述したように、対流に関係する対流熱伝達係数Hcと、熱の電磁波放射である放射熱伝達係数Hrがあります。その中の対流熱伝達係数Hcを表すBデバイスは少なくとも、上面、下面、垂直面に対応する3個を用意する必要があります。
また、放射熱伝達係数Hrには絶対温度(K)がパラメータとして入ってきますので安易なミスを防ぐには、回路図全体の温度設定は絶対温度で統一した方が良いでしょう。一方、代表長さで高さ制限がついているのは係数2.51を算出したときの制限事項によるものですが、あまり厳密に考える必要はありません。
もっとも0.5mを超える高さのヒートシンクを電子回路で使用するとは考えにくいので迷うことは少ないと思いますが……。
Copyright © ITmedia, Inc. All Rights Reserved.
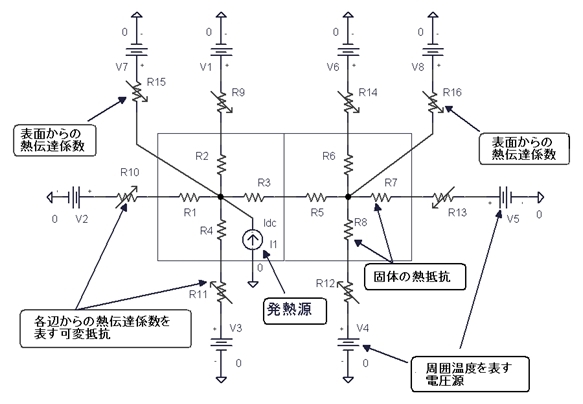 図1 熱抵抗回路網法のイメージ回路図
図1 熱抵抗回路網法のイメージ回路図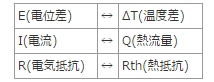 表1 回路と熱のパラメータの対応
表1 回路と熱のパラメータの対応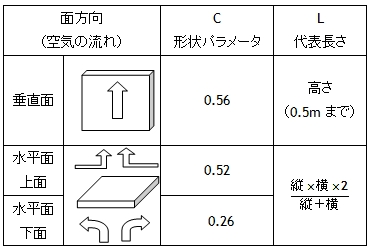 表2 対流熱伝達係数Hcの形状パラメータ
表2 対流熱伝達係数Hcの形状パラメータ
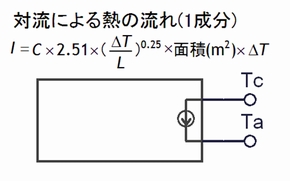 図2 対流熱伝達係数の実装例
図2 対流熱伝達係数の実装例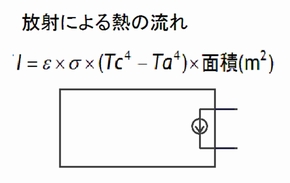 図3 放射熱伝達係数の実装例
図3 放射熱伝達係数の実装例


