フェライト（6） ―― トランス・チョークの設計：中堅技術者に贈る電子部品“徹底”活用講座（6）（1/3 ページ）

フェライト編最終回となる今回は、前回の結果から得られるコアの新しい設計パラメーターを紹介し、RCC用トランスや平滑用チョークの設計に適用した例について説明していきます。

[加藤博二（Sifoen），EDN Japan]

　前回の「磁気回路の基本式」の近似式に具体的な値を代入してみると、
AL　 ＝1.25×Ae/lg　（単位　mm、nH/T²）
N･I_sat＝280×lg　　 （単位　mm、Bms=0.35テスラ、AT）
となり、簡単な数字になりますのでこれらの数字はフェライトの基本的な数字として覚えておいてください。

　今回は前回の結果から得られるコアの新しい設計パラメーターを紹介し、RCC用トランスや平滑用チョークの設計に適用した例について説明していきます。

RCC用トランスコアの計算式

　RCC^＊）用トランスの動作を次の記号で表します。

P：電力　　E：動作電圧　　T_on：ON時間　　f：発振周波数　　AL：インダクション係数
N･I_sat：飽和起磁力　　δ：1次側通電時比率　　I_P：1次電流ピーク値
N：1次巻線巻回数　　L：RCC用トランスの1次インダクタンス

　RCCはトランスをチョークとして用いることで1次側のON期間中にコアに磁気エネルギーを蓄積し、OFF期間中にそのエネルギーを磁気結合した他の巻線に伝達(放出)します。
　トランスが1サイクルで受け渡しするエネルギーJは1/2 L･I_P²で表され、この現象が1秒間にf回（Hz）行われて電力P（W）を伝達しますから電力Pを表す式は1式となります。

　1式にI_P＝E/L×t_onと、t_on＝δ/fを代入すると、1式は2式のように書き換えられます。

　2式から発振周波数fや電力Pから1次インダクタンスLを求める3式が得られます。

　しかし、必要なL値が決まってもAL値（L＝AL×N²）やNはコアギャップlgをいくらにするかによっても変わりますし、加えてコアには磁気飽和に関するパラメーターN･I_satがあり、この値もlgの影響を受けます。
　つまり、δを仮定して発振周波数fからL値を仮設定したら、

lg仮定⇒AL値⇒巻回数N⇒1次電流ピーク値I_P⇒N･I_sat判定⇒lg変更⇒……

という繰り返しのループ計算を行う必要があり、最適値の決定までに何回も繰り返し計算が必要になります。

＊）RCC用トランスを取り上げたのはフィード・フォワード型や、他励フライバック型のような周波数固定型では発生しない周波数変動やギャップの依存性など、コアの総合的な計算が求められているためです。
　RCCとはRinging-Choke-Converterの略称です。時として回路構成が類似のブロッキングオシレーターと混用される時もありますが動作原理が異なりますのでWebサイトなどで両者の違いをご確認ください。
　またRCCコンバーターと称することは“コンバーター”が重なりますので誤用です。

パワーファクタK_Pの導入

　ここでRCC用トランスがチョークとして動作していることに着目して1式を変形すると、

となり、L･I_P²の最大値はALとN･I_satのみで決まることが分かります。
　つまり、コアのギャップ特性(lg～AL、lg～N･I_sat)曲線からあらかじめlg～K_P曲線を作成しておけば、電力P、発振周波数fから直ちに必要なギャップ長lgが分かります。

　このパラメーターK_Pはコイルの実験値であるL･I²積と結果的に等価ですが、4式から分かるようにlg～AL曲線とlg～N･I_sat曲線から導かれる、ギャップ長lgで決まる理論的パラメーターですから新しく、パワーファクタK_Pと呼ぶことにします。

　このK_Pの式に前回のALとN･I_satの近似式を代入するとKPの近似式は5式になります。

Kp≒0.1×lg×Ae　(mJ/Hz)　　単位mm　Bms=0.35 (テスラ)

図1：FEER35Aコアのギャップ特性（KP追加） （クリックで拡大）

　5式からRCC用トランスの最大電力はコアのBmsの2乗とギャップ空間体積(=lg×Ae)が左右することが分かり、またコア(Ae､Bms)が決まっている場合のギャップ長の概略値を求めることができます。
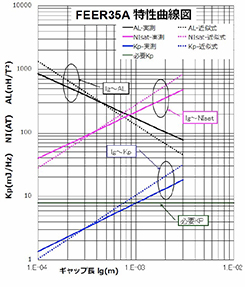
　図1は従来のコアのギャップ特性に上記のK_P曲線を追加したものですが、この3本の曲線群が設計に必要な曲線になります。
注）5式は空間がエネルギーを「持つ」のではなく、空間が「制御する」という意味です。磁気エネルギーはコアに蓄積されます。