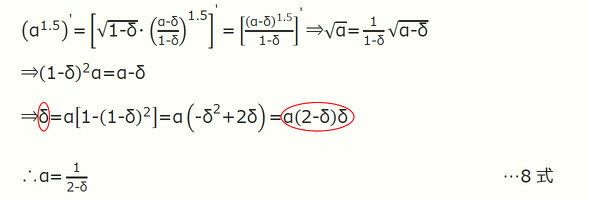ジャンクション温度の計算（3）―― 任意の三角形損失の温度計算：中堅技術者に贈る電子部品“徹底”活用講座（77）（2/4 ページ）

[加藤博二（Sifoen），EDN Japan]

損失形状が任意の三角形の場合

　上述したように波形を計算可能な成分に分解し、各成分の個別の温度上昇を合算することで矩形波以外の損失波形の温度上昇も求められることが分かりました。
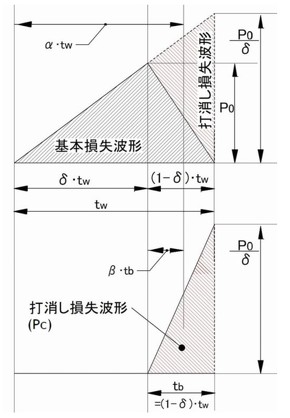
　この結果を踏まえて通常の三角形の定義について図2を基に検討します。図2においてαは図1と同じく温度を計算する時間比、δは損失ピーク位置の時間比であり波形の形状パラメーターです。
　図1との違いは、

①打ち消される側の損失波形が矩形であるか三角形であるか。そして、
②δ経過後に打ち消し用の三角形の損失が適用される

図2：三角形の定義［クリックで拡大］

の2点だけでありその他の計算の流れは同じです。

　図2の図式解法から時刻δの位置でピーク損失P₀になる波形はt_Wの時刻（終了時）でP₀/δの損失になる三角形の一部と見なせます。この増加形三角形損失を基本損失波形とします。
したがって損失が減少する時刻δより後は基本損失波形と、印加時間［(1−δ)･t_W］、ピーク損失P₀/δで表される打ち消し損失P_Cの合成と見なします。
（簡略化のため(1−δ)･t_W＝t_bとします）

　計算の主な流れは次のようになります。

1）時刻α･t_Wでの基本損失による温度上昇ΔT₁
　時刻（α･t_W）での温度上昇ΔT₁は2式に倣った5式になります。

2）アバランシェ波形の計算例に倣ってδ以後の打ち消し波形P_Cの計算位置をβとします。
　時刻β･t_b［t_b＝(1-δ)･t_W］での打ち消し損失P_Cによる温度上昇ΔT₂は6式です。

3）βは7式でパラメーターαと関係付けられます。
　図2下段の打ち消し用三角形の計算位置βは、

　　β･tb＝β･(1−δ)･t_W　　です。

　このβの位置は同図上段の全体像から計算位置αとピーク損失位置δの時間差（Δt）であることが分かります。つまり、

　　Δt＝(α−δ)･t_W　　です。

　両者は同じ時間位置ですから等号で結び、βについて解くと7式になります。ただしα＞δです。

4）温度がピークになる時は5式と6式の時間変化率が等しくなる時ですからそれぞれをαで微分して等しくなる条件を求めます。簡略化のために各式で同じ係数（□部）は省略します。

　8式に代表的なδを代入すると次のようになります。
　　δ＝0　　（減少形）　　⇒α＝0.5　　⇒減少中の中点で最高温度になり、そして
　　δ＝0.5　 （対称形）　　⇒α＝2/3　　⇒下降の途中で最高温度になります。また
　　δ＝1　　（増加形）　　⇒α＝1　　　⇒波形の終端で最高温度になります。