ジャンクション温度の計算（3）―― 任意の三角形損失の温度計算：中堅技術者に贈る電子部品“徹底”活用講座（77）（4/4 ページ）

[加藤博二（Sifoen），EDN Japan]

従来の近似法との比較

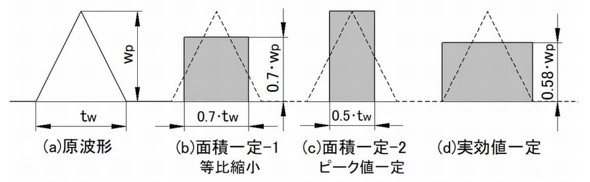
　図4に従来、資料などで公開されてきた三角形（δ＝0.5）の矩形波近似の手法をまとめてみました。図4（b）、（c）は原波形（a）を面積一定（平均値一定）で換算したものであり、（d）は実効値換算（1/√3）したものです。
　しかしながらそれぞれの温度上昇ΔTは次のように微妙に異なってきます。

（a）→ΔT＝2/3√（2-0.5）　＝0.544（理論値）
（b）→ΔT＝0.7×√0.7　　　＝0.586（等比縮小）
（c）→ΔT＝1×√0.5　　　　＝0.707（時間縮小）
（d）→ΔT＝0.58×1　　　　＝0.58（実効値一定）

　加えて図4の近似法では三角形の形状（δ）によってΔTが変化する事象が反映されていません。波形の変化を含んで安全側で判断するのであればパルス幅t_W、損失W_P･(2/3)の矩形波（δ＝1、増加形三角形相当）に換算することが一番安全ですが＋20％程度の誤差を生じます（図3）。
　これらの背景から高精度に温度を予測する必要がある場合にはピーク位置も含めて近似することが重要になります。

図4：従来の近似法［クリックで拡大］

　今回は基本となる増加形の三角形の損失と重ね合わせの理を使用して三角形の形状を任意の三角形へ拡張することを考えました。その結果、三角形の形状によっては最高温度に達する時間位置や最高温度に違いが出ることが分かりました。
　計算式を多く用いましたが決して高度な式を用いているわけではなく、簡単な式のみで構成されていますので一度は計算をしてみてください。理解が進むと思います。

（注意）
　本稿では過渡熱抵抗は√(t)に比例していると仮定していますのでこの条件から外れると計算結果は異なってきます。このことを無視すると得られた結果の信頼性はなくなりますので適用条件には気を付けてください。

　今回は任意の三角形の損失波形の温度上昇について説明をしてきました。その結果同じピーク損失であっても三角形の形状によって温度上昇係数は0.471〜0.667まで＋40％近く変化することが分かりました。
　前回、波形を近似する時には10％程度の誤差が生じるという話をしましたが今回の計算から分かるように波形の近似にはピーク損失だけではなく、そのピーク位置も重要になります。この点を踏まえて波形を近似してください。

　ここまではより計算が簡単である直線的損失変化の温度上昇について説明してきました。次回は損失が直線的ではなく正弦波で表される事例について検討を進めます。

---

執筆者プロフィール

加藤　博二（かとう　ひろじ）

1951年生まれ。1972年に松下電器産業（現パナソニック）に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。

⇒連載『中堅技術者に贈る電子部品“徹底”活用講座』バックナンバー