ステップダウン形DC/DCコンバーターの設計(2):たった2つの式で始めるDC/DCコンバーターの設計(4)(1/4 ページ)
今回は前回の検討で得られた各部の波形からスイッチング動作に関係する素子に要求される特性項目と値について説明します。
前回は既に説明した2つの式を使って基本的なステップダウン形DC/DCコンバーターの設計に着手しました。またキャパシターの理解を深めるためにエネルギー消失問題について1つの考え方を示しました。
今回は前回の検討で得られた各部の波形からスイッチング動作に関係する素子に要求される特性項目と値について説明します。
今回用いる式はテーマとした2つの式からは導けない経験式が主体になりますが、「経験式とはこんなものか」の程度に理解してください。
半導体の温度計算
DC/DCコンバーターの設計を進めていく途中で必要になるのが半導体の定格の決め方です。電圧、電流定格は動作波形を基準にすればディレーティングを考慮してFETを選択できますが、半導体にはもう一つの定格、温度定格があります。
この温度はジャンクション温度(Tj)やチャネル温度(Tch)で定義されているために直接測定できません。したがってどうしてもケースやヒートシンクなどの外部測定値から計算で求めることになります。
その測るべき半導体のチップは図1(a)に示すように、コムと呼ばれる銅製の金属板上に高温はんだで取り付けられており、さらに全体が絶縁性の樹脂でモールド(成形)された形をとっています。実機ではこの半導体をユーザーが基板やヒートシンクに取り付けて使用します。
したがってチップで発生した熱は高温はんだ〜コム〜モールド樹脂〜ヒートシンクを経由して大気などに放熱されますがFETなどのカタログで半導体メーカーが保証している熱抵抗*1は図1(a)に示す、チップとパッケージ取り付け面との間の熱抵抗Rth(J-C)のみです。
ここでヒートシンクの大気に対する熱抵抗をRth(H)とすれば、チップからみた大気までの熱抵抗Rthの合計は図1(b)に示すように損失(=熱流量)が伝わっていく経路の2つの熱抵抗の和[Rth(J-C)+Rth(H)]になります。この場合の大気とチップ間の温度差ΔTは熱流量を電流Iに、そして熱抵抗Rthを抵抗Rに置き換えた1式*2で求められますがこの式はオームの法則(E=I×R)の式と同じ形です。
本稿のテーマとした「2つの式」以外になりますが電気系の技術者ならオームの式と同じですから違和感はないはずです。
このチップの温度ははんだの温度を左右し、はんだの故障率や信頼性に影響します。
この観点からはんだ温度は90℃以下に抑えたいのでリードや端子部の温度は90℃とします。したがって機器内の温度を50℃とすれば許される温度上昇は40℃以内にしなければなりません。
*1 物体に熱流量(=損失)が流れると温度差が発生しますがこの時の物体の特性値を熱抵抗と言います。
*2 厳密にはヒートシンクと半導体の間のグリスなどの接触熱抵抗もありますがここではRth(H)に含めることにします。
Copyright © ITmedia, Inc. All Rights Reserved.

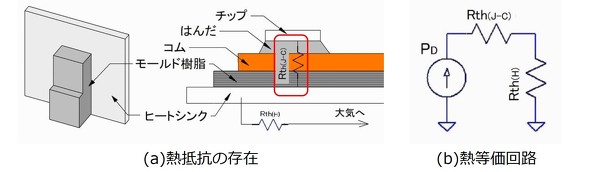 図1:FETの放熱図
図1:FETの放熱図


