ステップアップ形DC/DCコンバーターの設計(3)CRスナバー回路とチョークの要求特性:たった2つの式で始めるDC/DCコンバーターの設計(10)(3/4 ページ)
CRスナバー回路の定数設定
上述したようにプリント基板のパターンには寄生インダクタンスLeが発生しますのでドレイン電流を急峻に遮断するとLeの両端にスパイク状の電圧が発生し、FETのVdss保証値を超えるとFETにダメージを与えます。このLeを考慮した回路図を図2に示します。
この回路の振る舞いは通常は初期条件付きの微分方程式を解いて求めますがそれでは本連載の「たった2つの式……」の趣旨から外れてしまいます。また実設計でも回路図には表記できなかった周辺素子の寄生容量、回路の動作速度、各素子の直並列損失、など計算に繰り込めないパラメーターの影響が多すぎて計算精度が向上しません。ここではLの式やCの式で用いたエネルギーの保存則から応答の傾向を求めてみます。
インダクタンスLやキャパシタンスCに蓄積されるエネルギーJL、JCはそれぞれ2式、3式で表されることは本連載の初めに説明しました。ここでIはインダクタンスの電流、Vはキャパシタンスの電圧です。
寄生インダクターLeに蓄積されたエネルギーJLが全てスナバー回路のキャパシターC2に移った場合、C2の充電電位Vは2式と3式を両立させた4式で求めることができます。
として
4式のIは寄生インダクターLeを流れるターンオフ時の電流ですからドレイン電流(図3)のIdpが相当し、VはVoutに重畳されるスパイク状の電圧ΔVPが相当します(図4)。
実際の動作としてはLeのエネルギーJLはFETのターンオフ損失として消費されたり、スナバー回路のR2で消費されたりします。この作用によって実際のΔVPは4式より減少します。
定性的にはR2が小さくなるとR2での損失が減少するのでΔVPは4式に近く(大きく)なり、逆にR2が大きいとスナバー回路が抵抗性になりますのでやはりΔVPが大きくなります。つまりR2には最適値があります。
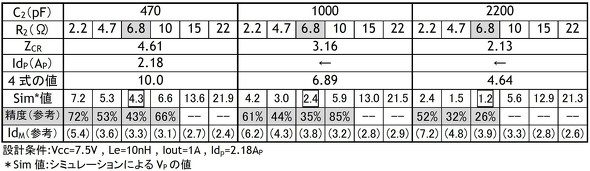
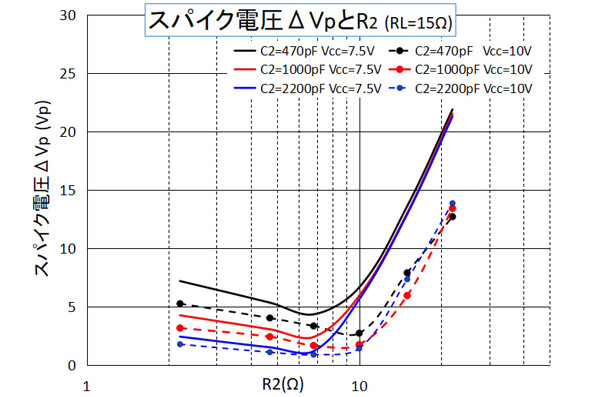
シミュレーションでの解析値を表2に、同じくグラフを図5に示します。同表では抵抗性の目安としてシミュレーション結果のΔVP値が4式を超える精度の項を“ーー”にしています。なおグラフ(図5)にはVcc=10V時の結果も追記しました。
C2、R2の効果は概略次のようになります。
(R2の効果)
・R2を小さくするとスパイク電圧ΔVPは4式の値に近づくとともにターンオンピーク電流IdMが大きくなります(表2)。
・R2を大きくするとスナバー回路が抵抗性になるためにIdMは減少しますがスナバー回路の効果が無くなるのでΔVPが大きくなります(図5)。この時、ΔVPはC2の影響を受けなくなります。
・電源電圧Vccが高いとIdMが減少しますのでΔVPが低下します。図4のVoutは一定ですからFETのVdsのピーク電圧VPはVccによっても影響を受けます。
(C2の効果)
・C2を大きくする(黒→赤→青)とΔVPは減少しますがドレイン電位の振幅成分もC2を流れるようになりますのでR2の損失も増加し変換効率が低下します。
・R2がZCRを超える付近からC2の影響は急速に減少しR2で決まる電圧に収れんしていきます。
このようにC2、R2とΔVPには依存性があり、表2や図5の結果からこの回路例ではR2がZCRの70〜100%程度の時にスパイク電圧ΔVPが最小になることが分かります。CRスナバー回路はうまく調整するとΔVPを低下させることができますが同時にΔVPが減少した分だけエネルギー保存則に従ってR2の損失は増加します。
最終的な定数はノイズ特性や温度上昇、変換効率を考慮して決めますが、FETのターンオフ時間やパターン形状が決まっていない設計初期からこれらの要因を配慮しても計算精度は上がりません。一方、形状が決まった最終段階で計算しても大幅な変更はもはやできません。
ですから設計初期段階では(Le・I2・f)とした概算損失でR2の発熱、温度上昇を見積もります(f:動作周波数)。
ここで1/2の係数が付いていないのはLeのエネルギーがC2に移る時と、C2に移った電荷が次のターンオン時にFETで放電される時の2回にわたってR2を通るためです。
ここで説明した各種のエネルギーは1回のスイッチングサイクル毎に発生するものですからコンバーターの動作周波数を上げればCRスナバー回路の損失も増加します。この損失はLeに起因しますので配線長を短くすることが有効です。近年ソリッド(固体)化されたDC/DCコンバーターが増えてきているのは使いやすさの面もありますが損失の面でも優位になります。
Copyright © ITmedia, Inc. All Rights Reserved.
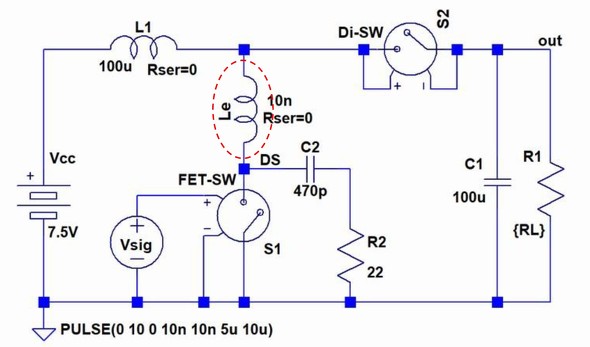 図2:Le(赤丸)を考慮したCRスナバー回路付ステップアップDC/DCコンバーター回路
図2:Le(赤丸)を考慮したCRスナバー回路付ステップアップDC/DCコンバーター回路

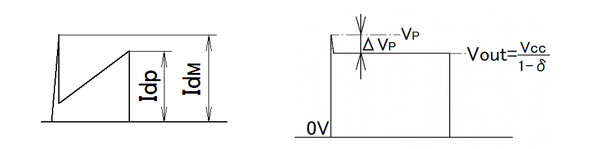 左=図3:ドレイン電流波形の記号
左=図3:ドレイン電流波形の記号