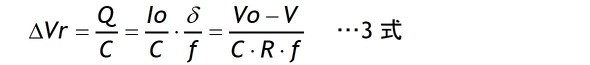ステップアップ形DC/DCコンバーターの設計(4)リップル電圧の図式解法/キャパシターの要求特性:たった2つの式で始めるDC/DCコンバーターの設計(11)(2/5 ページ)
リップル電圧の図式解法
この項は「2つの式」を離れて図1に示す基本回路図から得られる各部の波形の図式解法でリップル電圧を求めていきます。ここで使用する式は図1の波形を表現するための式であり基本は1次式ですから図と照らし合わせれば式の意味は容易に理解できます。
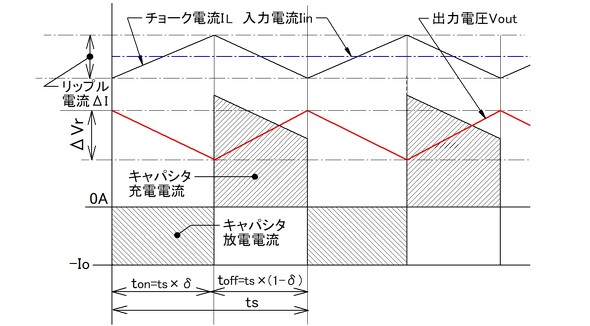
①ton期間(ts×δ)中はFET-SW(S1)がオン、Di-SW(S2)がオフですからキャパシターC1は放電し両端電圧Voutは降下します。
そして
②toff期間[ts×(1-δ)]中は各スイッチの状態が入れ替わりキャパシターC1は充電され、Voutは上昇します。
上記の関係を図2に示します。図2から分かるように、ton期間中にQ=Io×tonの電荷がキャパシターから負荷に供給されΔVrだけキャパシターの電圧は低下します。その後、放電された電荷はtoff期間中にチョークL1から供給されされ初期の電圧まで回復(上昇)します。
キャパシターC1を出入りする電荷Qは図2の各斜線部の面積に相当します。チョークによるC1への充電電流は台形波ですがここでは面積計算が簡単なton時の方形面積*を計算します。
*定常状態では充電電荷=放電電荷です
Qの定義はQ=i×tですから
ここで時比率δは δ=(Vo-Vcc)/Voであり、リップル電圧ΔVrは電荷Qを電圧に換算したものです。これらの関係からリップル電圧ΔVrはCの定義式(C=Q/V)に従って3式で計算できます。
3式からリップル電圧ΔVrは負荷抵抗Rに反比例し、入出力電位差に比例することが分かります。またチョークL1の値には無関係です。この点は出力電圧やL値でリップル電圧が変動するステップダウンコンバーターの様子とは異なります。
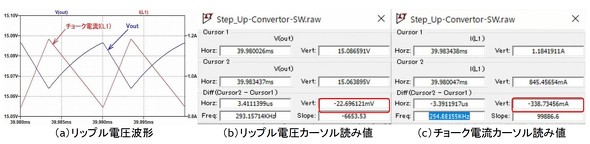
シミュレーションでの確認
LT-Spiceに次の定数(V=10V、δ=0.33、L=100μ、C=100μ、ts=10μs、R1=22.5)を設定し動作を確認します。表1に計算とシミュレーション結果を示しますが両者は誤差1〜3%の精度で一致していると分かります。
Copyright © ITmedia, Inc. All Rights Reserved.
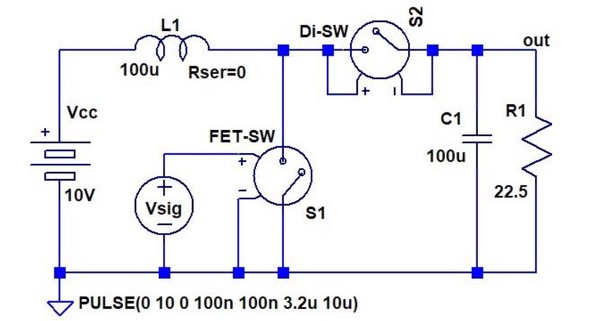 図1:基本回路図
図1:基本回路図