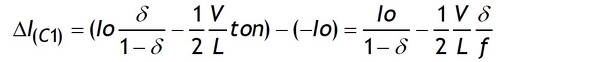ステップアップ形DC/DCコンバーターの設計(4)リップル電圧の図式解法/キャパシターの要求特性:たった2つの式で始めるDC/DCコンバーターの設計(11)(3/5 ページ)
実際のリップル電圧
ここまで説明してきた内容は全てキャパシターに理論(理想)値を設定しています。しかし、前シリーズのステップダウンコンバーターの章で説明したように、実際にキャパシターC1に多用されるアルミ電解コンデンサーにはESR(等価直列抵抗)と呼ばれる無視できない抵抗成分が存在します。より実態に近いリップル電圧を計算するにはこのESRの影響も考慮しなければなりません。
このキャパシターC1には図4に示すように台形波(状)電流が流れます。C1が理論通りの純キャパシター(ESR=0)であれば今まで説明したように台形波電流でも平滑化(積分)されてリップル電圧は三角波状になります。ですがESR成分に発生する電圧には前述の平滑作用はなくDC的な(ESR×電流)の電圧変動が発生します。キャパシターC1にESRを設定した時のリップル電圧波形ΔVr(=Vout)と電流波形I(C1)を図4に示します。
オン期間(ton)が始まってS1がターンオンするとC1から放電が始まるのでESRによる電圧降下が生じます。
逆にオフ期間(toff)が始まるとC1はチョークL1から充電されますのでESRによる電圧上昇が生じると同時にL1、C1、ESRの共振が生じます。
実際のリップル電圧ΔVrは出力電圧Voutの微少電圧変動です。図4から分かるようにオフ期間(toff)中の電圧の変化(上昇)はESRによって段差を生じています。続く波形はESRとC1、L1の各値が成すLCR共振の振動が始まり厳密な計算には振動を表す式が必要になります。
ですが実機での測定誤差を考えると設計時にはそのような計算精度は必要なく、もう少し簡易的、かつ実用的な方法を考えます。
キャパシターC1の充電時は前述のようにLCRの共振を起こして電圧波形が変動しますがC1が放電するオン期間(ton)中の電圧降下のテーパー(傾斜)そのものにはほとんど差は生じません。
これはton期間中のC1の電圧降が負荷電流Ioによる電荷の放電によるものであり、実際のスケールで見た場合、1サイクル中では負荷電流Ioはほぼ定電流と見なせます。ですからキャパシターのESRが変動しても電圧波形が上下に移動するのみで傾斜には影響しません。従ってこの変動の様子からリップル電圧ΔVrを計算した方が共振の影響を受けないので計算精度が向上します。
次にチョーク電流の様子について考えます。
負荷へのエネルギーはtoff期間中のみに供給されるため、チョーク電流のtoff期間中の電流IL(OFF)は波形の面積平均値が出力電流Ioにならなければなりません。従ってIL(OFF)の中心(平均)値は「Io/(1−δ)」になります。また定常であるという条件からton期間中の電流IL(ON)の中心値も「Io/(1−δ)」になります。
つまりチョーク電流ILは「Io/(1−δ)」を中心に変化しており、チョーク電流ILの最小値IL(MIN)は中心値「Io/(1−δ)」から電流のテーパー分(ΔI)の1/2を引いたものです。これらの関係を式で表せば4式になります。
ここでVはコンバーターの入力電圧です。
そしてターンオン時のキャパシターC1の電流I(C1)のプラス領域からマイナス領域の電流変化幅は図1や図4に示すようにIL(MIN)と同じ*になります。
従ってESRを考慮したリップル電圧を表す式は5式となります。5式の第2項はC1に流れる4式の電流によるターンオン時の電圧変化(降下)分です。
具体的にシミュレーションに用いた図1の定数では“ΔVr=0.0222+ESR×0.8335”になります。表2に計算値と第1項、第2項の成分を比較しますが各成分および、合計値ともに良好な一致を見せています。
*キャパシターC1の電流波形はチョーク電流のAC成分ですから電流振幅はチョーク電流と同一です。計算による確認ではターンオン時の電流振幅ΔI(C1)は次のようになります。
ton期間中は負荷R1にはC1からのみ電流が供給されるのでC1の放電電流はIoであり、放電電荷量Q(ON)はIo×tonです。この電荷は次のtoff期間にチョークから充電されます。
このtoff期間中に充電される電荷Q(OFF)をtoff期間の平均電流IXに換算するとQ(OFF)=IX×toffです。これら2条件から
が成り立ちます。実波形ではこの平均電流IXからチョーク電流の変動ΔIの1/2を引いたものがターンオン直前のC1への充電電流値です(チョーク電流の交流成分は全てC1に流れる)。
求めるC1の電流振幅ΔI(C1)はこの値とton期間の放電電流(Io)との差分です。この式は4式と同一です。
Copyright © ITmedia, Inc. All Rights Reserved.
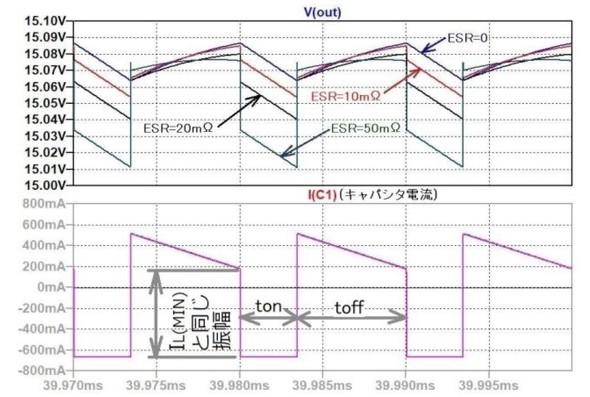 図4:ESR別リップル電圧波形
図4:ESR別リップル電圧波形
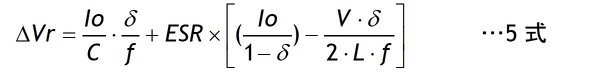
 表2:リップル電圧の比較
表2:リップル電圧の比較