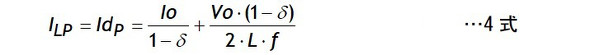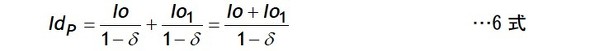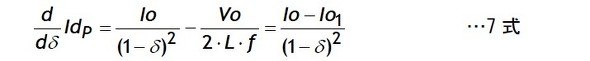反転形DC/DCコンバーターの設計（2）部品の定格：たった2つの式で始めるDC/DCコンバーターの設計（16）（2/5 ページ）

[加藤博二（Sifoen），EDN Japan]

Id_PのV_CC依存性

　台形波状になっているFETの電流Id_Pはどの入力条件で最大値になるのでしょうか？ 台形波を「矩形波＋三角波」と考えた場合、矩形波と三角波の比率はどのように変わっていくのでしょうか？

　定常的なFETのドレイン電流のピークId_Pを次のように考えます。最初に3式のI_LPを安定化制御されたVo、Ioを使って4式で表します。

　ただし4式にはチョーク電流連続モード時に限るという制約条件が付いています。この「電流連続モード」が成立するためには一定値以上の負荷電流Ioが必要になり、この下限の電流値をIo₁とします。
　このIo₁は別稿で説明しますが5式で求められます。

　この5式を4式に代入して整理したものが6式です。5式と6式から同じ入出力条件でもL×fによってIo₁を通じてId_Pは変化することが分かります。

　前述の4式をδで微分してIdPの増減の様子を調べると電流連続モード（Io＞Io₁）の範囲では4式のId_Pはδの増加とともに単調的に増加していくことが分かります。V_CCとδは負の相関関係なのでIdPを求める時はV_CC(MIN)、Io_(MAX)の条件で測定しなければなりません。このIo_(MAX)には過電流保護回路動作時の最大値を含みます。

※参考までに4式の微分結果を7式に示します。

　7式から電流連続モード（Io＞Io₁）の範囲では7式は正なので、Id_Pは単調増加であることが分かります。

Id_Mの計算、測定

　ノイズ抑制のためにFET-SWのドレインーソース間にCRスナバー回路を付加した場合、2式のId_Mは7式で計算されるピーク電流に達する時もあるので、後に続く整流ダイオードD₁の寄生容量C_AKも計算に含めなければなりません（R₂はCRスナバー回路の抵抗値）。
　しかし、このC_AKは電圧依存の非直線性特性を持つので計算に取り込むことは困難です。一般には8式を使ってId_Mを概略計算した後に仮の品番のFETを用いて実測し、その値から周辺定数を調整します。