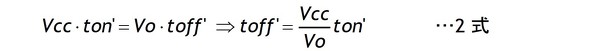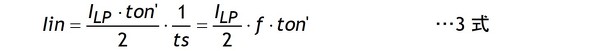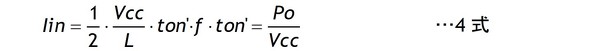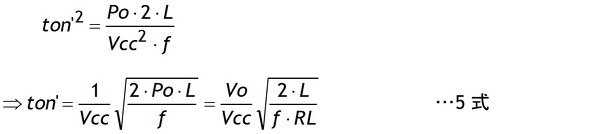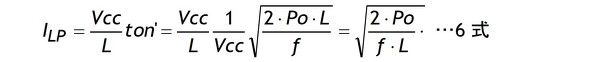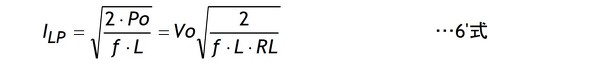反転形DC/DCコンバーターの設計（4）不連続モードの振る舞い：たった2つの式で始めるDC/DCコンバーターの設計（18）（1/3 ページ）

[加藤博二（Sifoen），EDN Japan]

【連載一覧はこちら↑↑↑】

　前回の記事中で「次回はリップル電圧の図式解法、キャパシターの要求特性について説明します」と予告しましたがリップルの説明は少し後回しにして、今回はチョークの電流連続性が途切れた場合のコンバーターの振る舞いについて説明します。ステップアップ型に倣って図形を表す1次式を基に「エネルギー保存則」を加えた2次方程式を通じて説明していきますが、ステップアップ型と同じなのは手順だけです。変数の値は同じものもあれば微妙に変わっているものもありますので注意してください。用語についても簡単に再度説明していきます。

電流不連続モード

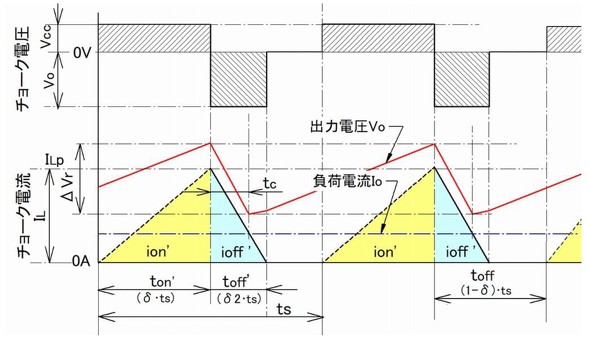
　電流不連続モードとは、図1に示すようにチョーク電流I_Lが1周期の中で途切れる区間が存在する動作モードのことです。
　無負荷に近い異常な軽負荷モード（仕様範囲外）の時に発生しますがコンバーター負荷の故障の一つとしてこのような故障モードもあり得ます。ですから対策をとる、とらないは別として、その時の振る舞いについては事前に把握、検討しておく必要があります。

　この軽負荷のモードの場合、制御スイッチのオン期間中にチョークに蓄積された磁気エネルギーが1周期中に消費できず、結果的に出力電圧Voを上昇させて磁気エネルギーを消費しようとします。どこまでVoが上昇するかはオン時間と出力電力［Vo²/RL］で決まります（RLは負荷抵抗）。
　この電圧上昇に伴ってオフ期間中のチョークの誘起電圧は増加するので磁気エネルギーの放出期間が短くなり、急速に減少したチョーク電流I_Lは底付きを起こし、電流が連続して流れなくなります。

チョーク電流不連続時の特性

　図1に電流不連続時のコンバーターの代表的な電圧･電流波形を示します。オフ時間にはエネルギー放出の時間toff’（＝δ₂）と、本来の遮断時間であるtoff（＝1−δ）の2種類の時間が存在します。そこで両者を区別するために不連続モード時のエネルギー授受時間はton’とtoff’のように“ ’ ”を付けて表します。
　ここで出てくる式は図形を表す1次式とLやCの基本式ですから図と比較すれば容易に理解できます。

図1：電流不連続時の各部電圧･電流波形［クリックで拡大］

　各式中の記号の定義は次の通りです。ton’期間中の電流変化Ion’は0Aから開始されるのでLの基本式である1式で計算できます。

　　I_LP：チョーク電流の最大値　　　L：チョークL1のインダクタンス値　　　I_L：チョーク電流
　　Iin：入力電流（DC）　　　　　　Vcc：入力電圧　　　　　　　 　　　　Vo：出力電圧
　　Io：出力電流（DC）　　　　　　 Po：出力電力　　　　　　　　　　　　RL：負荷抵抗

　一方、toff’は図1の状態が定常なので電圧･時間積の関係を使って2式で計算できます。

　入力電流Iinは図1の◢領域（Ion’）の1周期平均として求めます。

　3式のI_LPに1式を代入します。出力電力Poを入力電圧Vccで除したものがIinですからIinを求める式は4式になります。

　4式をton’について解いて5式を得ます。

　5式からton’が一定値に固定されている場合は出力電圧Voが√(R)に比例する負荷依存性を持つことが分かります。ton’が一定ということはチョークにたまる磁気エネルギーも一定ですから当然の帰結として負荷抵抗RLによらず電力Poも一定になります。
　逆に言えば出力電圧Voを一定に保つためには√(Po)に対応してton’を制御しなければなりませんが、Po→0でton’→0に漸近するので理論的に無負荷には対応できません。最小限の疑似負荷か、周波数fをPoに対応して減少させる工夫が必要になります。

　5式でton’が決まったので5式を使ってLの基本式（1式）からI_LPを求めます。

　あるいは6式をVoで表した6’式を使用する時もあります（Po＝Vo²/RL）。

　6式から、I_LPはVccに関係なく電力Poにのみ左右されることが分かります。この5式、6式は不連続モード時の変換電力Poが（チョークの磁気エネルギー×周波数）であることからも導くことができます。