レギュレータのモデル化:Signal Integrity
スイッチングレギュレータは非常に便利なモジュールである。「変換効率に優れている」ことが最大の特徴だが、「モデル化が容易である」という点も注目に値する。
図1は、米Texas Instruments社のスイッチングレギュレータ「PTH08T220W」の代表的な特性試験結果を示したものである。負荷電流の定常値が8A、最大変化率dI/dtが2.5A/μsのステップ状の変化に対する応答を表している。下側のプロットが負荷電流特性であり、上側のプロットが同レギュレータの電圧応答特性である。
ここで、このレギュレータの回路モデルを作成することを考えてみる。その際、レギュレータ内部の情報は必要ない。基本的な回路モデルを作成するだけなら、図1のステップ応答特性から十分な情報を得ることができる。
図2に示したのが、基本的な回路モデルである。理想的な電圧源VREFと基板上のVccとの間に接続された抵抗R1とインダクタンスL1が、レギュレータの主な特性を表現する素子だ。コンデンサC2、抵抗R2、インダクタL2は、出力コンデンサの特性を表す。
回路モデルの中で最も直接的に値を求められるのはR1である。図1のように、ステップの立ち上がり部分から100μsを越える領域では、回路はDC的な動作に落ち着いている。この領域ではコンデンサC2には定常電流はほとんど流れないので、C2の部分は開放状態にあると考えることができる。同様に、L1も短絡というDC動作特性に置き換えることが可能だ。従って、動作特性に影響する素子はR1のみとなる。このことから、出力電圧の低下、言い換えれば定常状態でのDCオフセット電圧が決まる。R1の値は、電圧の降下分と負荷電流との比から求められる。
ステップの降下部分に当たる250μs以降の領域では、L1とC2の効果が現れ、正弦波的な減衰振動が発生する。このレギュレータのアプリケーションノートには、出力コンデンサを1200μFにしたときの典型的なステップ応答特性が示されている。それに倣い、C2を1200μFに設定して、正弦波的な減衰振動波形の幅に合致するようにL1の値を決めればよい。
最後に、得られたR1、C2、L1に対し、正弦波的な減衰振動のダンピングファクタが合致するようにR2の値を決める。R2の値が決まったということは、メーカーがステップ応答特性を取得するときに使用した回路のESR(equivalent series resistor:等価直列抵抗)の値が得られたことを意味する。
残るはL2である。この基本的な回路モデルは、DCから約100kHzまでの範囲におけるレギュレータの動作を表したものだといえ、この低速ステップ応答特性からは、L2の値を決めるのに必要な情報は得られない。この周波数範囲を超えると、コンデンサC2のESL(equivalent series inductance:等価直列インダクタンス)であるL2の影響が出始めるのだ。言い換えれば、低周波領域のモデルにおいては、L2の値は0としておけばよいということである。
このような基本回路モデルは、主要極帰還型(dominant pole feedback)のレギュレータであればどれにでも適用できる。多重極位相補償帰還型(multipole phase compensating feedback)のレギュレータ(実際にはほとんど存在しないだろう)以外であれば、この等価回路は有効だといえる。
メーカーから提供される設計指針に従って出力コンデンサの容量値とESRを最小にするのは非常に重要なことである。そうしなければ帰還回路が発振し、回路が破壊してしまうこともある。図2はそうした意味でのレギュレータの動作をモデル化したものではないので、その点には注意されたい。
<筆者紹介>
Howard Johnson
Howard Johnson氏はSignal Consultingの学術博士。Oxford大学などで、デジタル・エンジニアを対象にしたテクニカル・ワークショップを頻繁に開催している。ご意見は次のアドレスまで。www.sigcon.comまたはhowie03@sigcon.com。
Copyright © ITmedia, Inc. All Rights Reserved.
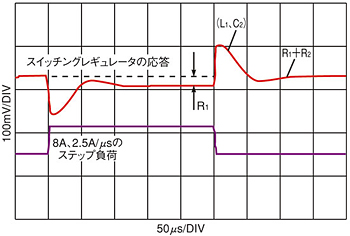 図1 スイッチングレギュレータのステップ応答(低周波領域)
図1 スイッチングレギュレータのステップ応答(低周波領域) 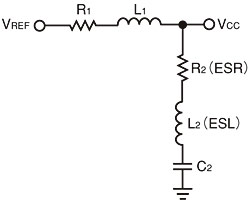 図2 スイッチングレギュレータのモデル このような簡単な回路により、ほとんどのスイッチングレギュレータをモデル化することができる。
図2 スイッチングレギュレータのモデル このような簡単な回路により、ほとんどのスイッチングレギュレータをモデル化することができる。



