これは便利! 2端子の発振回路「シリアルオシレータ」:Wired,Weird(3/4 ページ)
シリアルオシレータの仕組み
シリアルオシレータの回路動作を説明しよう。トランジスタQ1のエミッタにはコンデンサC1が接続されており電源投入の初期電圧は0Vである。この時 Q1のベースには電源電圧の半分のVcc/2の電圧がかかっている。このためトランジスタQ1のベースには逆電圧がかかり、ベース電流は流れず、Q1はオフしている。トランジスタQ2はQ1がオンした時にベース電流が流れてオンする。従って初期状態ではQ1、Q2ともOFFしている。電源投入後に、コンデンサC1は電源から抵抗R5、R4、R1を通して充電され、Q1のエミッタ電圧は徐々に上昇する。エミッタ電圧がVcc/2+約0.5Vの電圧になると、Q1のベースに電流が流れ始め、Q1がオンして、Q2にベース電流が流れ、Q2もオンする。
Q2がオンすると、LEDに電流が流れLEDは点灯する。またQ1のベースは抵抗R2を通してQ2のコレクタに接続され、ほぼ0Vになる。Q1のエミッタ電圧には充電完了時のC1の電圧が残っており、Q1にはベース電流が流れ続け、オン状態を維持する。その後、コンデンサC1の電荷はQ1のコレクタからQ2のベース電流となって短時間で放電される。
コンデンサC1の電圧がQ2のオンを維持できる電圧(約0.8V) まで放電すると、Q2はオン状態が維持できなくなり、Q2のコレクタ電圧が上昇し始める。これに伴いQ1のベース電圧が上がり、Q1は急激にオフし、Q2へのベース電流が無くなってQ2がオフし、LEDが消灯する。
その後、コンデンサC1は約0.8Vの電圧から再び充電が始まり、Q1のエミッタ電圧がVcc/2+約0.5Vの電圧まで上昇すると、Q1のベースに電流が流れ、Q1がオン、Q2もオンする。このような動作を繰り返してシリアルオシレータは発振する。この回路の発振波形を図4に示す。
図4のCH1はQ2のコレクタ波形、CH2はQ1のエミッタ波形(C1の充放電波形)である。C1が約0.8Vから充電され、約2.8Vに達するとコンデンサが急速放電する。この放電時にLEDが瞬灯する。放電する波形の拡大図を図5に示す。
放電時間はコンデンサ容量と電源電圧、負荷の重さで決まる
図5のCH1の波形からLEDの点灯(瞬灯)時間は約25ms程度であることが分かる。このシリアルオシレータの回路では、コンデンサC1の充電時間(消灯)が長く放電時間(点灯)が短いのでLEDがフラッシュ点滅動作になる。発振周期はほぼコンデンサC1の充電時間と放電時間で決まる。充電時間の計算式はT=C*R*(LN(Vcc/(Vcc-Vth1))−LN(Vcc/(Vcc-Vth2)))となる。Vccは電源電圧 Vthはしきい値電圧でVth=Vcc/2+Vbe(約0.5V)になる。Vcc=5V Vth1=2.8V Vth2=0.8Vを入れて計算すると、LNの値は0.67となり、T=10*10^-6×1*10^5×0.67=670msで計算される。これに放電時間を追加すると約700msになり、部品のバラつきを含めると、実測の770msとほぼ符合する。放電時間はコンデンサC1の容量と電源電圧と負荷の重さで決まり、正確な計算式にするのは難しい。
いい仕事をする抵抗器
さて、図2の抵抗R5の役割であるが、この回路でのトッピング的な2つの役割を果たす。1つ目はC1の充電時にLEDには微小電流が流れるため薄く点灯してしまうが、これを防いでLEDを完全消灯させ、消灯と点灯時の光の変化(インパクト)を大きくする。2つ目はLEDの消灯時の電圧降下をなくし、低い電源電圧でも回路の動作を可能にする。この抵抗R5がないと微小電流が流れる時にLEDの電圧降下が発生しシリアルオシレータ部に印加される電圧が低下する。しかしR5を付加することで微小電流はR5に流れ電圧降下が小さくなり、シリアルオシレータに電源とほぼ同じ電圧が供給され、低い電源電圧でも発振動作できるようになる。その結果、電池で動かす回路では、電池寿命を長くできる。抵抗R5を外した波形を図6に示す。図4と比較すると抵抗R5の効果がよく分かる。
図6は図4と同じスケールであるが波形の振幅が小さくなり、周期は長くなっていることが分かるだろう。この波形ではシリアルオシレータ部分に供給される電圧が約2Vに低下し、C1の充電波形も約1.4Vまで下がっていることが分かる。これはLEDの微量電流時の電圧降下分の電圧の約3Vが発生したためである。抵抗R5の効果は、微小電流時の負荷の電圧降下を小さくし、発振回路部分の電圧を高くすることである。3Vの電池を使った回路でも順電圧が3V程度の白色LEDの点滅を可能にすることができる。つまり、電池の能力を100%引き出し、電池の寿命を長くできる。
Copyright © ITmedia, Inc. All Rights Reserved.
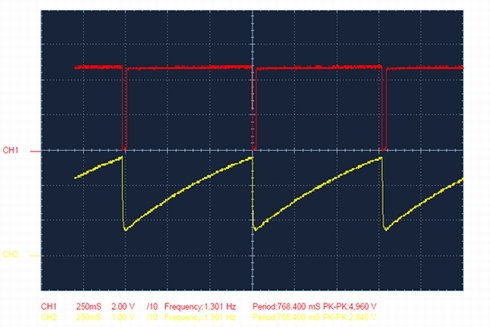 【図4】CH1はQ2のコレクタ波形、CH2はQ1のエミッタ波形(C1の充放電波形)
【図4】CH1はQ2のコレクタ波形、CH2はQ1のエミッタ波形(C1の充放電波形)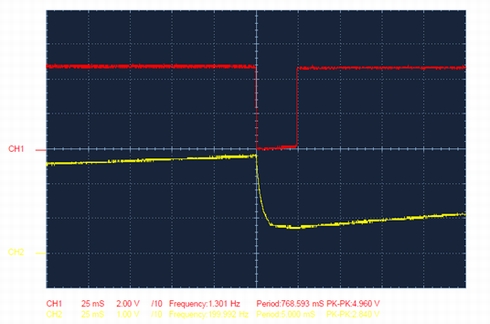 【図5】放電する波形の拡大図
【図5】放電する波形の拡大図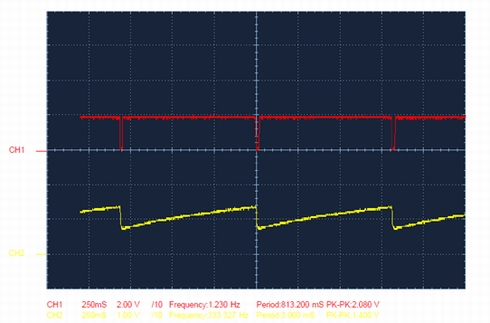 【図6】抵抗「R5」を外した波形
【図6】抵抗「R5」を外した波形


