SPICE応用設計（その6）：W.C.解析の注意点：SPICEの仕組みとその活用設計（17）（3/4 ページ）

[加藤博二（Sifoen），EDN Japan]

解析手法の妥当性確認（validation）

　前回の説明で使用した電圧増幅回路では最悪値を求めることができ、今回の図3の回路では最悪値を求めることができないことから回路の振る舞いに差があると考えられます。

　原因を切り分けるため、図3の各因子がV(RES)に及ぼす影響具合をそれぞれ単独で検証します。

　VCOは入力電圧に応じて正弦波を出力するだけなので外部から見ればAC電源と等価と考えることができます。確認のために解析回路(図3)のVCO部分をAC電源に置き換え次の解析を実行してみました。

　周波数掃引範囲はVCOのバラツキである100±10KHz(90K〜110KHz)です。

図5　LC共振回路の周波数特性と定数依存性 (クリックで拡大)

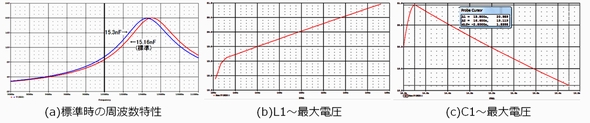
　図5(a)は周波数特性(AC解析)、(b)と(c)はL1、C1のパラメトリック解析結果で、f=90K〜110KHzの中でのV(RES)の最大値をプロットしています。

　この図5を見てみると、

1）同図(a)から、標準状態でのV(RES)が最大になる周波数は100K〜110KHzの間にある

2）さらに、C1が標準より1％大きくなると100KHz時の電圧は上昇する
（この結果から前述のリスト1の"C_C1…(Increased)"の結果が計算されています）

3）同図(b)から、L1は大きいほど最大電圧が高くなる

4）同図(c)から、C1は13.8nF時に最大になる（注：最大/最小時ではない）

ということが分かります。

この結果は、

• 図5(c)のC1依存性にピークを生じているのはC1最小では共振周波数が周波数範囲の上限範囲を超えてしまい、掃引周波数範囲内では共振できなくなるからであり、
• L1(TYP)＝151.6μH、fMAX＝110KHz、の条件で共振できる容量はC1=13.808nFである。（グラフと合致）

と回路の動作から説明することができます。

　つまり、両端の条件がピークになるのはL1のみで、周波数やC1は両端ではピークにならず、いわゆる単調関数ではないのです。

　このため、

手法(A)の感度解析法では感度の方向性を見誤り、

手法(B)のランダム偏差法ではピーク点を見逃していた

というわけです。

　単調関数でない場合にはワーストケース解析だけでは歯が立たないのです。

　そして、このようなことを防ぐためには今回用いたようにモンテカルロ解析も併用しなければなりません。

「モンテカルロ解析で工程能力を把握し、ワーストケース解析で極限値を把握する」

　解析にあたって、このような方針が必要になるのは当然ですが、それでも"すべてうまく解析できるか？"と問われると一抹の不安が残ります。

　今回の事例ではワーストケースの解析結果がバラツキの上限と著しくかけ離れていたために容易に結果の異常に気付くことができましたが、ワーストケース解析の値がモンテカルロ解析のバラツキ上限近辺にあり、なおかつ、モンテカルロ解析の回数が少なく結果が粗い場合には正しく解析できたか、否かを見分けることは困難です。

　やはり、回路が単調関数になっているか、共振特性を示していないか、などの回路の素性を下調べしておくことは欠かせません。

　理論的にはL＝Max/C＝Minが最大値の条件ですが共振点が周波数範囲変動の中に入っている必要があります。

　確認すると、

L=166.76μH(＋10％)　　C＝13.644nF(△10％)　　f＝105.5KHz(ω0)　　の時で、

共振の鋭さQは

Q＝ωL/R＝22.11　　です。

　この値がV(RES)の最悪値として検出されなければならないのですが、特に感度解析法ではC1の方向性も誤って検出していますので結果の食い違いが大きくなってしまっています。

　一方、モンテカルロ解析の結果は前述の通り

L＝160.3μH(＋5.7％)　　C＝13.6nF(△9.7％)　　f＝107.27KHz(＋7.3％)　　の時V(RES)=21.577V_P

であり、理論解に近い値(97.6％)を得ることができています。この両者は互いに補完関係にあり、併用することが望ましいのです。

　解析結果の"V&V"にはこのように結果を矛盾なく説明できなくてはなりません。また、必要に応じて今回のように異なる解析手法の併用が必要になる時もあります。

　この点を忘れ、ツールに解析機能が備わっているからと言ってむやみに機能を過信すると思わぬ結果となる時がありますのでしっぺ返しをもらわないように注意が必要です。

　本連載でのテーマである「分かって設計する」の"分かって"の部分は決して回路や部品の特性のみを指して言っているのではありません。

　今回の例のように、ツールや回路、部品の特性(個性)も分かっていなければならないことの他に、どのようなモデルをどのような物理法則で解くのかというモデル化手法もvalidation(妥当性確認)の一因を成します。巻末にそのような観点でまとめたコラムを作成しましたのでSpiceの世界ではあまり問われることのないモデル化のvalidationの例として一読ください。

　次回はワーストケース解析の意味するものをもう少しお話するとともに今まで取り上げてこなかった解析機能について説明していきます。