SPICE応用設計（その6）：W.C.解析の注意点：SPICEの仕組みとその活用設計（17）（4/4 ページ）

[加藤博二（Sifoen），EDN Japan]

エネルギー保存則は破れたのか？
（モデル化手法のvalidation）

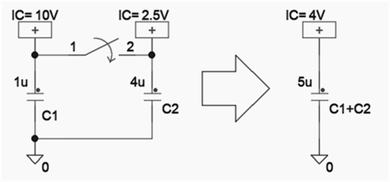
　図Aの例題回路に示すように、

キャパシタC1　1μF−10V

キャパシタC2　4μF−2.5V

に充電されたものをt＝0で短絡し、その後の状態を求めます。思考実験ですから指定のない限り、短絡スピードやL、R成分は考えません。

図A　例題回路

　電荷保存則だけを考えれば図Aの通り4Vで安定しますが、このときの静電エネルギーは

SW-ON前：50μJ＋12.5μJ ⇔ SW-ON後:40μJ

となり、差し引き22.5μJだけSW-ON前後で合致しません。エネルギー保存則は破れたのでしょうか？

　ここで鍵になってくるのが問題のモデル化手法で、まずLやRで短絡した時の極限値を考えます。

• Rで短絡する場合はRの値によらず22.5μJが消費されるのは簡単に求められますが、R=0では不明です。
• Lで短絡する場合はエネルギーが消費されないので図Aの答えにはなり得ませんし、L=0では磁気エネルギーが蓄積できませんのでL＝0とlim(L→0)ではモードが不連続です。ちょうど、Y＝AX＋BとX＝C(垂線)のような差です。
  （Y＝AX＋BにはY軸との交点が存在しますが、垂線には交点が存在しません）

　このままでは、どう工夫しても『LやRの極限値を採る』という考え方では上手く説明できそうもありません。

　次に、前提にする物理法則としてMaxwell方程式から導かれる『空間のエネルギー流を伴うエネルギー保存則』を考えます。

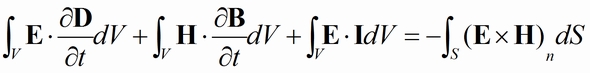（電気磁気学　電気学会発行　1968年11月20日　第7版より）
※右辺の電磁波の流れは空間Vへ流入する方向が「＋」なので「−」は空間Vから流出する方向です。
（V:対象空間、S:空間Vの表面、E:電場、D:電束密度、H:磁場、B:磁束密度、I:電流密度）

　左辺の第1項は電場のエネルギー流、第2項は磁場のエネルギー流、第3項はジュール熱の、それぞれの総量です。

　一方、右辺は面Snを出入りするポインティング・ベクトル(電磁波のエネルギーの流れ)の総量を示しています。

　この新しい保存則による解析モデルとしては次の2つのモデルが考えられます。

【1】右辺の存在を考慮しない場合(右辺＝0)

　空間へのエネルギーの出入りがないので素子間のエネルギー授受だけを対象にした従来のエネルギー保存則です。電気回路の多くはこの条件で解かれています。

【2】右辺の存在を考慮する場合(右辺≠0)

　［電場のエネルギー流］＋［磁場のエネルギー流］＋［ジュール熱］が右辺のポインティング・ベクトルに従って電磁波として空間へ散逸していきます。

　図Aでは解析対象は電場(キャパシタ)だけでジュール熱成分が"0"(R＝0)ですから左辺が有限値になり、電磁波を考慮しない【1】の従来のモデルでは等号が成立しません。したがって【2】の電場のエネルギーの変化(22.5μJ)が空間に磁場の変化を誘起し、磁場の変化→電場の変化→磁場の変化…という電磁波になって空間へ伝播していくモデルで解析することになります。モデルのvalidationとは物理法則を含む時もあるのです。

　※現実の問題では配線や部品内部にRやLが微少といえども存在しますので時定数が構成され、空間に漏れる電磁波のエネルギーは極微量になりますので【1】のモデルで解いても実用上の差異は認められません。
（アンテナや導波管など電磁波のエネルギを対象にする場合を除く）

---

執筆者プロフィール

加藤　博二（かとう　ひろじ）

1951年生まれ。1972年に松下電器産業（現パナソニック）に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。