Spiceの新しい応用解析:自然対流問題(その3):SPICEの仕組みとその活用設計(21)(2/4 ページ)
半導体の熱モデル*2)の作り方
前回は単一材料の均一温度としての解析を検討してきましたが、実際は簡単なヒートシンク実装例でもヒートシンクと半導体が組み合わされていて、熱の流れを考慮するとジャンクション〜取り付け面、および、ジャンクション〜表示面間で数℃の差が生じます。均一材料とした上で実際との差分を理解して結果を読み取れば問題はないのですが解析を行った人以外にその旨を理解することは困難ですのでCFDツールと同様に半導体モデルも2抵抗モデルとして作成します。
*2)熱モデルとは温度解析を行う場合に用いる解析用モデルのことを言います。ちょうど、回路の動作解析に用いるモデルをSpiceモデルと言うように、温度解析を行う時に用いる、どの箇所にどのような熱抵抗が配置されているかを表しているのが熱モデルです。
半導体の例として“TO−220F”の内部構造図(図2)とその等価熱抵抗(図3)の分布を例として取り上げ熱モデルの作り方を紹介します。
TO220Fの代表的な寸法は10mm(W)×15mm(H)×5mm(D)であり、一般的な許容損失は40Wです。発熱は半導体であるチップと呼ばれるシリコン部材に集中発生し、他の部材に熱が流れていく形態を取ります。
そして、チップは銅コムと呼ばれる熱拡散板兼構造材に搭載された上でモールド材(主としてエポキシ樹脂)に取り囲まれている構造になっています。
もちろん、銅コムはチップに直接触れていますので帯電しており、そのままでは扱いにくいのでモールド材で絶縁をしている訳です。
TO220Fは松下電子部品と松下電子工業(いずれも当時)が世界で最初に開発した絶縁型パッケージです。
実際の形状はこのような簡単な立方体形状ではなく、段付きの複雑な形状をしているのですが、細かい形状を再現しても結果には影響をあまり与えませんのでこのような簡易形状を採用しています。
チップ〜取り付け面間の熱抵抗Rth(j−c)
半導体のカタログで表示される許容損失(Pc,Pd、など)はこの半導体チップと取り付け面間の温度差が規定温度になった場合の損失を表しますのでカタログからRth(j−c)は計算で求めることができます。
ΔT(j−c)=Pc×Rth(j−c) ですから、TO−220Fとして一般的な40Wクラスの例では
ΔT(j−c) :125K(Tj=150℃、Tc=25℃)
Pc :40W
として、Rth(j−c)=125/40=3.125(K/W)です。
チップ〜表示面間の熱抵抗Rth(j−ca)
次に、Rth(j−ca)はモールド材の熱抵抗ですから
で求めます。
λ=3,厚み=5mm、面積=10×15mmを代入すると
です。
この熱抵抗Rth(j−ca)を通って表面まで流れてきた熱はここから空気へ流れていきます。
自立の場合のパッケージ表面の熱抵抗Rth(pkg)は代表的なカタログ値で計算できます。自立の場合の許容損失Pc0は1.5W程度(Tj=150℃、Ta=25℃)ですから、これらの値から、
Rth(pkg)=125÷1.5=83.3K/W 程度になります。
しかし、この空気への熱抵抗Rth(pkg)は自立している状態での測定ですので、全周囲面積として取り付け面も含んで熱抵抗が計算されています。本来はこの取り付け面の分だけを全周囲面積から差し引かねばならないのですが、簡易的に面積半減とし、求めたRth(pkg)の2倍の値をRth(c−a)として採用します。
従って、Rth(c−a)=83.3×2=166.6(K/W)になりますが、この値にはチップ〜ケース表面間の熱抵抗分Rth(j−ca)が既に含まれていますのでその分を考慮して、ケース表面からはRth(c−a)=166.6−11.1=155.6K/Wとします。
半導体の形状にはこの他にも種々ありますので計算した結果のみを表1に記します。
| TO−220F | TO−220FL*3) | TO−3P | ブリッジダイオード | ||
|---|---|---|---|---|---|
| サイズ | W | 10 | 10 | 15 | 30 |
| H | 15 | 8 | 20 | 20 | |
| D | 5 | 5 | 5 | 5 | |
| 許容損失 | 40W | 40W | 125W | (カタログ値) 1.5 |
|
| Rth(j−c) | 3.125 | 3.125 | 1.0 | ||
| Rth(j−ca) | 11.1 | 20.83 | 5.56 | 2.78 | |
| Rth(pkg) | 83.33 | 120.15 | 47.0 | 26.37 | |
| Rth(c−a) | 155.6 | 219.5 | 88.4 | 50.0 | |
| *3)TO−220FL:Fin−Lessの略称です。代表図は図4の通りで、一般的なTO−220ABパッケージからフィン部分を切り取った形状です。ブリッジダイオードは一般的な600V/20AクラスのSIP形状(Single−Inline−Pakage)のものとしています。(SIP形状のダイオードは松下電子部品と新電元工業が共同開発したものです) | |||||
Rth(j−ca)は各部寸法からTO−220Fの場合と同様に計算できますのでRth(c−a)の場合について各モデルの計算例を次に記します。ここではカタログの自立の温度〜許容損失曲線から直接Rth(pkg)を求めています。条件はエポキシ樹脂の熱伝導率λ=3.0、温度変化ΔTj=100(K)、周囲温度50℃、放射率ε=0.9です。
- TO−220FL:ΔT=100Kになる損失Pcは0.832292Wですので
Rth(pkg)=100/0.832292=120.15(K/W)
∴Rth(c−a)=2×120.15−20.83=219.47(K/W)
- TO−3P:ΔT=100Kになる損失Pcは2.1281Wですので
Rth(pkg)=100/2.1281=47.0(K/W)
∴Rth(c−a)=2×47−5.56=88.4(K/W)
- ダイオード:ΔT=100Kになる損失PDは3.7958Wですので
Rth(pkg)=100/3.7958=26.37(K/W)
∴Rth(c−a)=2×26.37−2.78=50.0(K/W)
このようにして求めた熱抵抗値を使って実際の構成に合わせた熱抵抗回路網を構成すれば解析が可能になります。今回はΔTjを統一して熱抵抗を算出しましたが、解析結果を基に熱の流れを反映した熱抵抗を算出し直せば結果の信頼性は高くなります。しかし、後述するように目立った改善はないようです。
Copyright © ITmedia, Inc. All Rights Reserved.
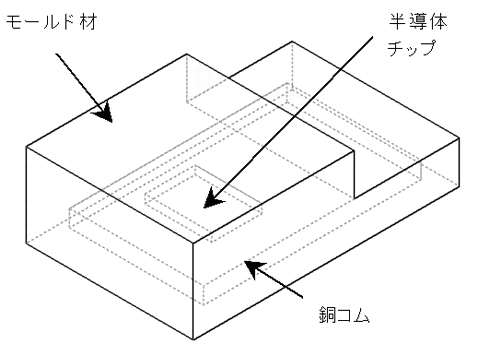 図2 TO220Fの熱抵抗モデル【構造図】
図2 TO220Fの熱抵抗モデル【構造図】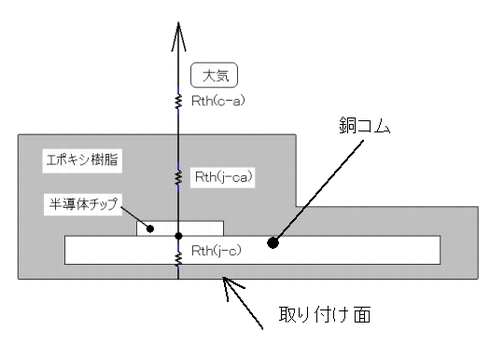 図3TO220Fの熱抵抗モデル【等価熱抵抗】
図3TO220Fの熱抵抗モデル【等価熱抵抗】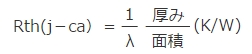
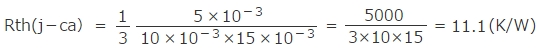
 図4 TO−220FL
図4 TO−220FL


