Spiceの新しい応用解析:自然対流問題(その3):SPICEの仕組みとその活用設計(21)(3/4 ページ)
アルミシャシーの平面方向の熱抵抗モデルの作り方
発熱源となる半導体類はこのようにして熱モデルを作成することができますが、これらの発熱源から出てくる熱流量を伝えるアルミシャシーの熱抵抗モデルはどのように考えたら良いのでしょうか?
単純に図5(a)のように、X,Y方向だけの流れを考えた場合には隣り合う2辺間(斜め方向)の熱の流れを表現できませんし、この平面ブロックに発熱を与えることができません。
次に図5(b)の灰色部のような三角モデルを考えます。中心を介して斜め方向への熱の流れも表現でき、中心部へ発熱を与えることができるので問題はなさそうです。
では灰色部の熱抵抗はどのように計算したら良いでしょうか?
ここで適用する法則は本連載の第19回で紹介した熱に関するフーリエの法則です(1式)。
1式に従えば、任意の位置xにおける微少長さdX分の熱抵抗dRは(三角形ですのでY寸法=aX)
となり、このdRを0〜Xの区間について積分すれば図5(b)のRhを求めることができます。
このように一見、図5(b)は正論のように見えるのですが、実際に計算してみると中心点は温度特異点になってしまい、計算することができません。
ここでは面に出入りする熱流量を中心に考え、図5(c)のように中心点から辺までの長方形のブロックを考えます。
この考え方であれば前述の図5(b)の問題を回避できます。
この考え方を4方向に適用した最終の熱モデルが図5(d)の最終モデル案です。
シャシーの温度分布計算例
図6〜9に参考資料1表7のモデルの詳細と温度分布の計算結果を引用します。
参考資料1の記載によれば各物性値は表2のように記載されています。
しかし、サイズは記載されていますが、各部品の位置関係までは記載されていませんので図を光学的に拡大し、拡大図から各位置関係を測定し、図9としました。そしてCFDツールの損失の与え方も明記されていませんでしたので参考資料1の文書や図7の構造図から中央の半導体と右側の3連半導体は取り付け面に発熱を与える手法で解析されていると仮定し、条件をそろえるために熱抵抗回路網法での解析もRth(j−c)を省略しました。
また、ブリッジダイオードの取り付け面樹脂厚はt=0.5とし、半導体についてはサイズからTO220FLの金属面がむき出しのものとしました。これらがアルミベース板と絶縁用樹脂(各t=0.5)に載って、アルミのシャシーに取り付けられているものとして次の手順で計算を行いました。
- アルミシャシーは4分割とし、その右下面に発熱源となる半導体がある。
- シャシーの空間への放熱抵抗は前回のRth_Plate.subで1.0045(K/W)でしたので4分割するとすれば各面は4.018(K/W)の放熱抵抗が各面の中心点から大気へ接続されているとしました。
- 1/4サイズの縦方向伝導の熱抵抗
62.5mm/(239×160mm×2mm)=0.817(K/W) - 1/4サイズの横方向伝導の熱抵抗
80mm/(239×125mm×2mm)=1.339(K/W) - ブリッジダイオードの樹脂部熱抵抗
0.5mm/(3×30mm×20mm)=0.2778(K/W)
(チップ〜ケース表面、ケース表面〜樹脂板の熱抵抗分) - 半導体の樹脂部熱抵抗も表1の通り20.83(K/W)、3連半導体は近似的に1/3の値を設定
- 半導体取り付け部は部品間のセンターでシャシーを切り分け、3分割して各部毎に算出後、組み合わせる。
- 樹脂板の下にあるアルミベース板の熱抵抗はλが樹脂部の79倍あるため、今回は無視します。
以上の結果を回路図としてまとめたものが図5です。同図にはSpiceの結果表示も重ねて表示してあります。
温度上昇値の解析結果は次の通りです。
図10、および表3の値は1回目の計算結果から各部の空気への放熱抵抗を修正した2回目の解析結果ですが、その効果は表3に示すように0.5K以下であり、概略の計算であれば修正する必要はなさそうです。
その精度ですが、測定各部は±2K以内に収まっておりCFDツールと良好な一致をみせています。この程度の違いであれば、どちらが正しいのかがはっきりとは分からなくなります。
ただし、今回は解析条件をCFDツールに合わせるために半導体のRth(j−c)を省略していますが省略しない場合は49.87〜57.67℃となって表3より3〜7K温度上昇が高くなります。しかし、この種の問題はモデルの作り方と精度のバランスをどう考えるかが左右する領域ですので設計者が決めれば良いかと思います。
Copyright © ITmedia, Inc. All Rights Reserved.
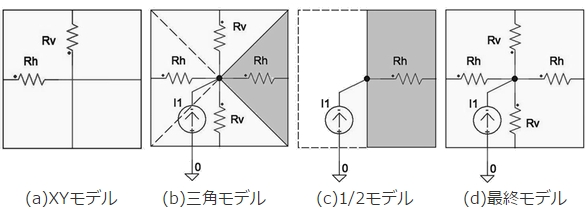 図5 平板の熱モデルの考え方
図5 平板の熱モデルの考え方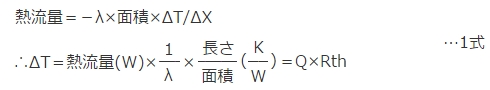
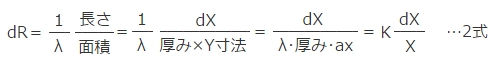
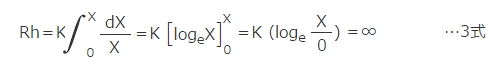
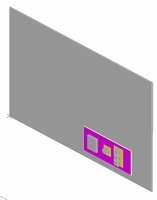
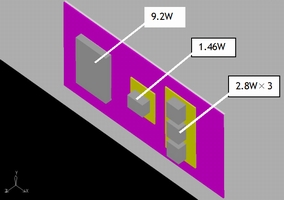 左=図6 モデル全体図 / 右=図7 損失分布
左=図6 モデル全体図 / 右=図7 損失分布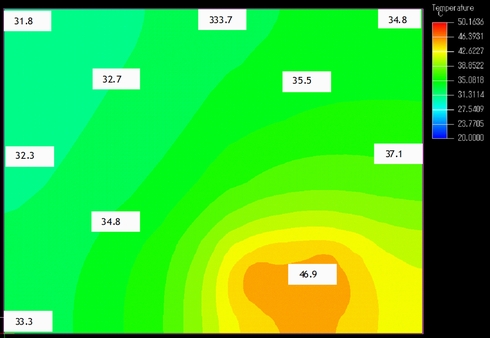
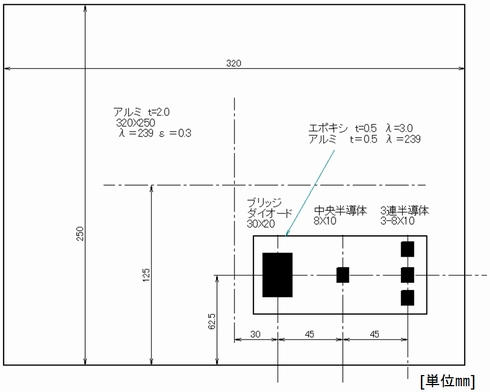
 表2 使用した寸法図・物性値
表2 使用した寸法図・物性値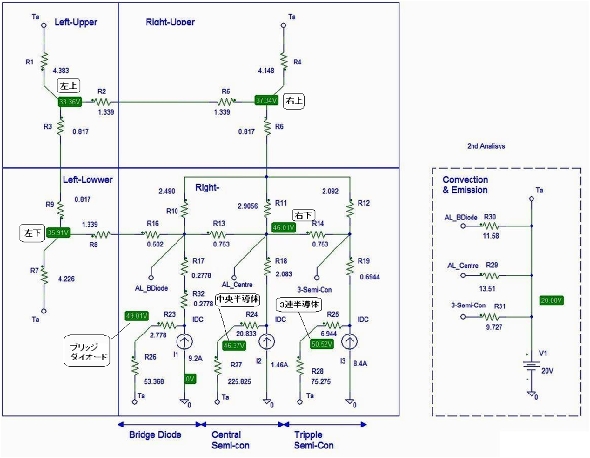
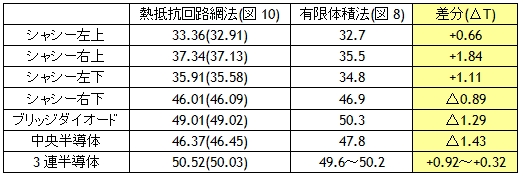 表3 精度比較 / ( )内は放熱抵抗修正前
表3 精度比較 / ( )内は放熱抵抗修正前


