ラプラス素子（その1）：SPICEの仕組みとその活用設計（23）（3/5 ページ）

[加藤博二（Sifoen），EDN Japan]

畳み込み積分

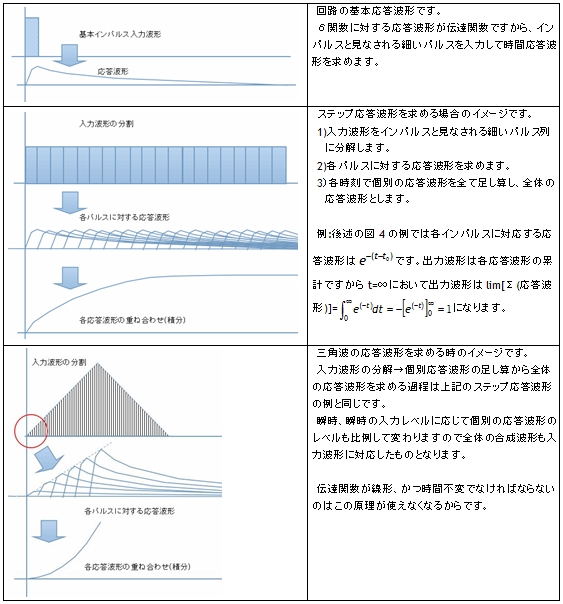
　4式と7式の比較から分かるように、ラプラス素子は本来、周波数領域の解析に使用するものですが、伝達関数のインパルス応答特性と入力波形をスキャンしながら積算する畳み込み積分を使用することで出力波形の時間応答波形を求める逆ラプラス変換の機能も有しており、そのイメージを表2に記します。

　ただし、この畳み込み積分が成立するためには伝達関数の特性が線形であり、かつ時間不変でなければなりません。AGC回路のように伝達特性が常に変わる場合には成立しないので適用回路には注意してください。

表2 畳み込み積分のイメージ （クリックで拡大）

　また、これらの原理から、伝達関数の注意事項として次の項目があります。

• 上記の単インパルス応答波形が解析時間内で減衰しない場合（応答が┏━型）は全体を足し算した時に発散します
• 伝達関数が高域まで延びている場合、単インパルス応答波形が時間と共に増大したり振動したりしますので解が安定しません

注）数値計算などの離散系においては連続関数ではなく厳密には総和なので「畳み込み和」というべきですが、この手法も通常は「畳み込み積分」と呼ばれています。