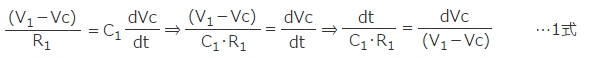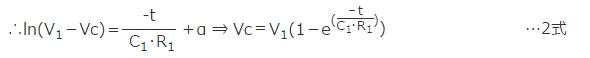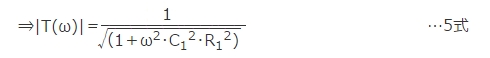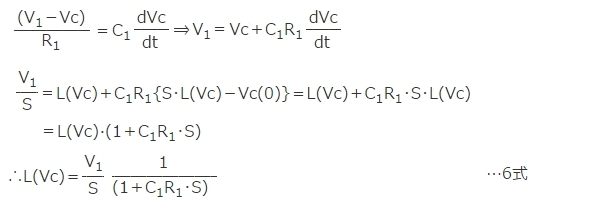ラプラス素子(その1):SPICEの仕組みとその活用設計(23)(2/5 ページ)
» 2015年04月23日 09時00分 公開
[加藤博二(Sifoen),EDN Japan]
デスクリート素子を使った過渡解析事例
ラプラス素子による解析に先立ち、Spice自身の精度を確認するために図1に示すCR積分回路による1次遅れ回路を解析的に解いてみます。
図1の回路図の電圧Vcついて微分方程式を立てて解くと1式、および2式のようになります。
ここでVcはC1の電圧であり、回路の初期条件はt=0でVc(0)=0です。
一方、周波数特性は回路方程式が3式ですので V1→Vc の伝達関数T(ω)は4式、5式のようになります。
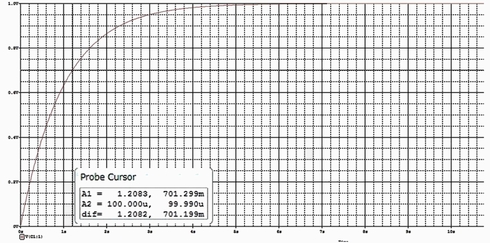
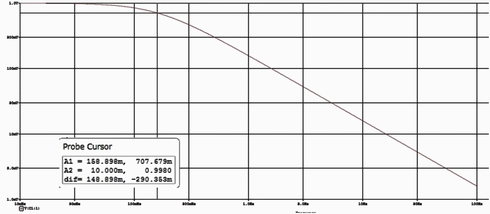
PSpiceによる図1の回路の過渡解析と周波数特性の実行結果を図2と図3に示します。
そして、そのプローブ画面からカーソルを使って値を読み取ってみました。
| 項目 | X軸 | カーソル値 | 理論値 | 誤差 |
|---|---|---|---|---|
| 過渡解析 | Time=1.2083秒 | Vc=0.701299V | Vc=0.701295V | +5.7×10−6 |
| 周波数特性 | f=0.158898Hz | |T(ω)|=0.707679 | |T(ω)|=0.707678 | +1.7×10−6 |
| 表1 PSpiceによる解析検証(CR積分回路による1次遅れ) | ||||
表1に示すように、PSpiceによる解と解析解は問題のない精度で合致していることが確認できましたので続いてラプラス変換と伝達関数の関係を見ていきます。
ラプラス変換を L() で表すとすれば回路の微分方程式である1式をラプラス変換した式は6式になります。
直流電源V1のラプラス変換は L(V1)=V1/S ですから V1→Vc への伝達関数T(S) は7式になります。
回路のインピーダンス比から求めた伝達関数(4式)と、ラプラス変換から求めた7式を比較すると両者とも同じ形になっていることが分るかと思います。
このような機械的な置き換え(jω←→S)に注目したのが前出のヘビサイドです。なお、6式の逆ラプラス変換による過渡応答の解は巻末コラムに示します。
Copyright © ITmedia, Inc. All Rights Reserved.
Special ContentsPR
特別協賛PR
スポンサーからのお知らせPR
Special ContentPR
Pickup ContentsPR
Special SitePR
あなたにおすすめの記事PR
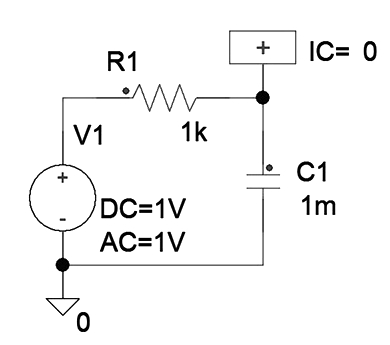 図1 1次遅れ回路
図1 1次遅れ回路