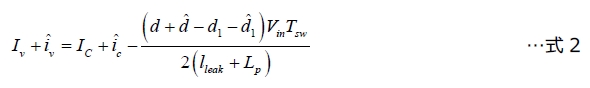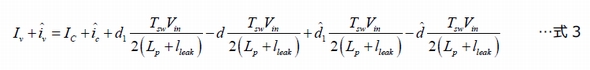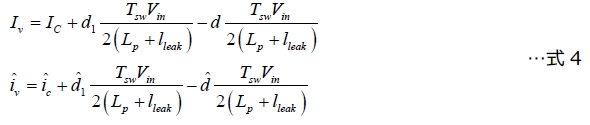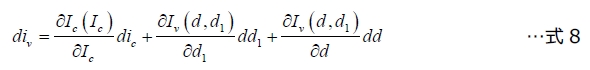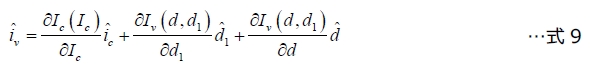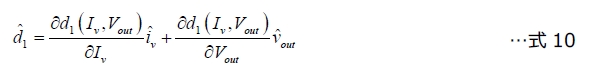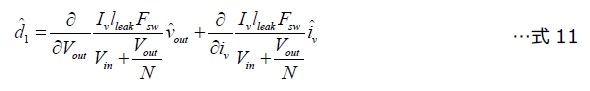漏れインダクタンスを使用したフライバックコンバーター（3） 小信号モデル化：電源設計（2/6 ページ）

[Christophe Basso（ON Semiconductor France SAS），EDN]

信号源の線形化

　これらの信号源を線形化する場合は、2つのオプションが利用できます。各変数に対して小規模な励起による変動を追加できます。小さい累乗記号「^」が付いた特定の変数がこれに該当します。AC項とDC項を整理して、静的な式と動的な式の2つの個別の式が形成できます。静的な式は動作ポイントを表します。このような式は実際ここでは必要ありません。ここで欲しい式は、もう1つの式である動的な式です。この手法の問題は、特に変数が3個以上の場合の項および、外積の数です。これらの項を整理してAC式とDC式を形成するのは煩雑な作業であり、ミスを生じる原因となる可能性があります。谷点電流の定義を試してみましょう。

　ここには、I_c、d、d₁の3つの変数があります。各変数に少量の変動を追加すると、次式が得られます。

　展開すると、次のようになります。

　ここでAC項とDC項を収集すると、次の2つの定義が得られます。

　次のように2つの係数k_ivdとk_ivd1を定義すると、

　式4に示す動的な式は、次のように整理できます。

　静的係数k_ivdとk_ivd1は回路図キャプチャーでパラメーターとして渡され、シミュレーションの開始前に評価されます。

　項を整理することなく、k_ivdやk_ivd1のような小信号係数をより迅速に取得する別のオプションも存在します。この例では選別操作は単純でしたが、式が複雑で多数の変数が存在する場合は、急激に実行困難となり、Mathcadのようなソルバーで自動化できなくなる可能性があります。より迅速な方法は、以下に示すように一連の非相関（独立）変数が与えられている状況で、偏微分を実行することです。

　または、小信号表記を使用します。

　ここで、AC項に対応する係数のみをこれらの偏微分から取得します。図2のd₁信号源にこの方法を適用すると、次式が得られます。

　この式は、次のように評価されます。

　k_d1voとk_d1ivの各係数について考慮すると、次のように式11を書き直すことができます。

　ここで、

　ここまで、d₁とI_vの各信号源を線形化したので、図2の回路を更新して簡略化することができます。結果を図4に示します。式5と式6および、式13と式14に示す各式は、パラメーター・テキスト・ウインドー内で計算されます。この図内にある全ての信号源は現段階でいずれも小信号タイプになっています。簡易AC解析を実行すると、周波数特性は振幅と位相の点で図3の周波数特性に完全に一致しています。