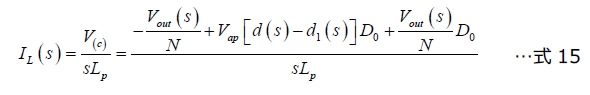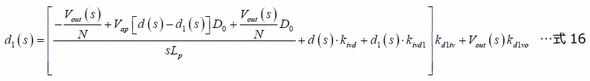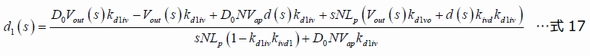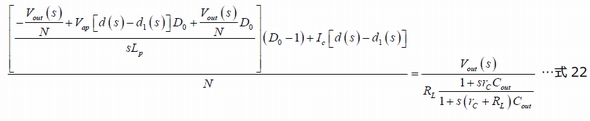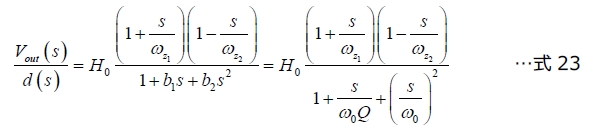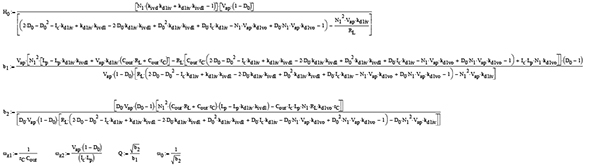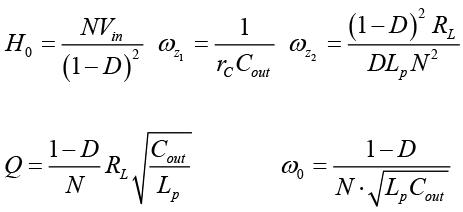漏れインダクタンスを使用したフライバックコンバーター（3） 小信号モデル化：電源設計（4/6 ページ）

[Christophe Basso（ON Semiconductor France SAS），EDN]

式の生成

　最初にインダクター電流を検討します。インダクター電流はノード「c」の電圧をインダクターのインピーダンスで除算した値です。ノード「c」の電圧は、電圧源B₁₀に直列となるノード「p」の電圧によって定義されます。ノード「p」の電圧は単純に、トランスの巻線比を通じて1次側に反射された出力電圧を差し引いた値です（ダイオードの順方向降下を無視）。次式が得られます。

　これまでにL_pを流れる電流が定義されている（図7のd₁信号源にあるI(Vc)）ので、信号源d₁を書き換えられます。

　d₁(s)についてこの式を解くと、次のようになります。

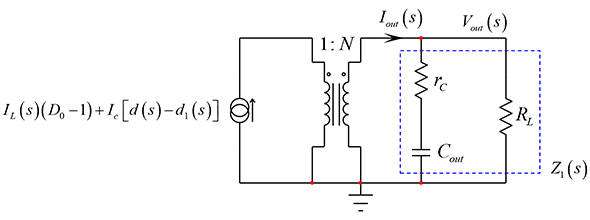
　出力電流は1次側電流をトランスの巻線比Nでスケール化した値です。これは電流源B₇によって定義される電流から、インダクターを流れる電流を減算した値で、式15で定義されます。

　この式で、I_cは本連載の第2回で既に定義されているDC値です。

　図9に示すように、この電流はr_C、C_out、負荷抵抗R_Lで形成されるインピーダンスを循環します。

図9：最終的には、出力コンデンサー、そのESRおよび、負荷抵抗R_Lで形成される複雑なインピーダンスをドライブするトランスが含まれる

　この出力電流は、次のように定義することもできます。

　インピーダンスZ1は、r_C＋C_outをR_Lと並列にするか、回路の高速分析手法（Fast Analytical Circuits Techniques：FACT）を適用する方法で、迅速に導くことができます。結果を整理すると、次式が得られます。

　ここで、式18、式20、式21の各式を組み合わせると、次式が得られます。

　ここでの関心事は、V_outを解き、伝達関数を整理して2次多項式にすることです。Mathcadを活用すると、次式が得られます。

　ここまで、以下の新しい係数を決定しました。

　文献に掲載されている、従来のフライバックコンバーターに関する伝達関数（漏れインダクタンスを含まない）は式23の形式に従い、以下の定義を使用しています。