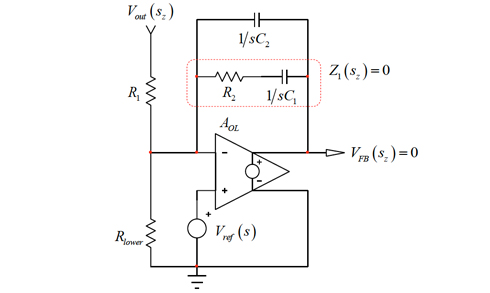
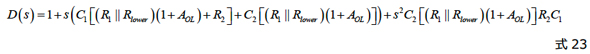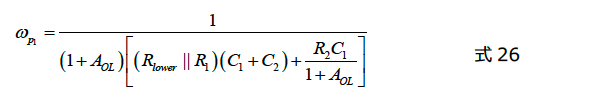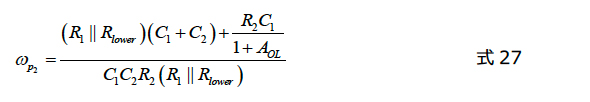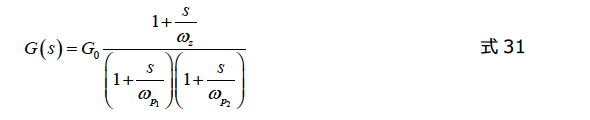オペアンプのダイナミック応答の検討（1） タイプ2補償回路の使用時：アナログ回路設計（5/6 ページ）

[Christophe Basso（ON Semiconductor France SAS），EDN]

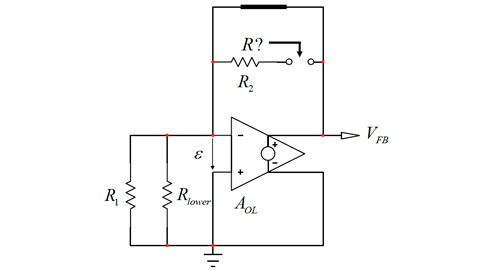
　2つの時定数が決まったので、2次の項に進むことができます。今度はτ₁²を求める必要があります。これはC₂を短絡で置き換えた状態で、C₁の端子から見た抵抗を意味します。図12に新しい回路を示します。R₂が関係するメッシュ内に単純な短絡を置いたので、合成抵抗Rは単純にR₂に等しくなります。

　これで終わりです。式12に従って複数の時定数を組み合わせると、分母D(s)を求めることができます。

図12：高周波係数はあいまいな表記を使用しているが最終的には何も複雑なことはなく、C₂を短絡しC₁の両端から見た抵抗を決定するだけである （クリックで拡大）

　品質係数Qが1よりもはるかに小さいと仮定すると、この2次形態を再構成することができます。その場合、両方の極は適切に分離されます。1つの極は低周波を支配し、2番目の極はスペクトルの上側領域に配置されます。式12から、2つの極が次のように定義されることを示すことができます。

　これらの定義を式23に適用し、整理および再構成すると、次の式が得られます。

　これで分母が求まりました。この回路にゼロは存在しているでしょうか。上記の対処方法を適用することができます。頭の中でC₁のみまたはC₂のみを短絡し、ついでC₁とC₂の両方を短絡します。これら3つの状況で、応答が存在しているでしょうか。C₁を短絡すると、R₂や他の抵抗が関係する単純な反転回路が得られます。C₁にゼロが関連付けられます。C₂を短絡した場合、オペアンプの出力はゼロになります。C₂に関連付けられるゼロは存在しません。両方のコンデンサーを短絡した場合も、もちろん応答は存在しません。ゼロの位置を決定するのに、図13で刺激つまり励起の伝播を阻止して、応答をゼロにできるのはどの素子ですか。C₁とR₂によって形成されるインピーダンスが実質上の短絡になると応答は消失します。

　この場合、

図13：R₂と直列接続されたC₁によって形成されるインピーダンスが実質上の短絡になると、応答はゼロになって、ゼロが形成される （クリックで拡大）

　この結果、次の位置でゼロが発生します。

　最終的な伝達関数は、次の式で表されます。

　ここで、