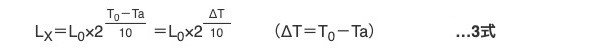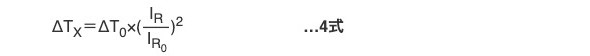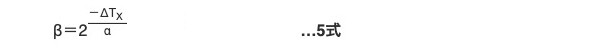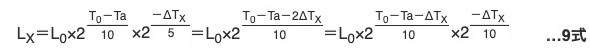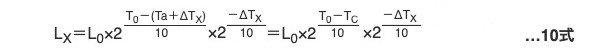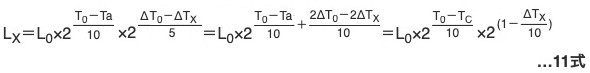アルミ電解コンデンサー（6）―― ドライアップ寿命：中堅技術者に贈る電子部品“徹底”活用講座（39）（2/3 ページ）

[加藤博二（Sifoen），EDN Japan]

実際の寿命計算

一般品の場合

　基本的には10℃2倍則で計算します。リップル電流I_Rがない場合が前提ですので最初に周囲温度Taから寿命L_Xを求めます。

　次にリップル電流I_Rが流れている場合は図2（a）のように中心温度がTaよりさらに高くなりますのでその影響を計算します。
　リップル電流による温度上昇の要因はジュール損ですからI_R²に比例します。
　したがって実際の缶の自己温度上昇ΔT_Xは

となりますが、このΔT_Xによる寿命への影響は10℃則ではなく、5式の加速係数αに関係します。α＝5℃の場合が多いのですがカタログなどの資料で値を確認してください。

　また、一般品にリップル電流を流すと中心温度が高くなりますのでΔT_Xによる効果βは5式のように寿命が短くなる方向へ作用します。つまり、ΔT_X＝αになるリップル電流を流すと寿命は半減します。

　上記の関係を組み合わせた最終的な寿命計算式は3〜5式を考慮した6式になります。

高周波品の場合

　リップル電流がない場合の基本的な寿命は一般品と同じであり、（a）の一般品との違いはリップル電流の条件が逆になっている点です。
　高周波品は定格リップル電流I_R0を流した条件で寿命L0が規定されています。したがって高周波品ではリップル電流を流さない場合は7式に示すように寿命が延びる方向へ効果βは作用しまので、（ΔT₀ｰΔT_X）＝αであれば寿命は2倍に延びます（ΔT_Xの計算は4式）。

　上記から最終的な寿命計算式は7式を考慮した8式になります。

缶表面温度T_Cによる寿命計算

　上記の寿命計算式に使用する周囲温度Taはどの位置で定義するかによって値が変わってきて汎用性のある値が定義できません。したがってアヤフヤな温度を使用するよりも実測した缶の表面温度T_Cを使用した方が再現性のある値が得られます。
　ここではα＝5℃、ΔT₀＝5℃とし、実測した缶の表面温度T_Cを用いた計算式を説明します。
　一般品の寿命計算式6式にα＝5℃を代入すると9式が得られます。

　この9式にTa+ΔT_X＝T_Cを代入すると10式になります。

　また高周波品の寿命計算式8式にこの考え方適用すると11式が得られます。

　なお、メーカーは自社の信頼性試験から算出された寿命推定式を推奨していますので上記の各式の適用についてはメーカーに確認をお願いします。
　また実際の温度測定に当っては次に示すような注意が必要です。

1. 缶表面温度T_Cの測定には感熱ラベル、赤外線温度計、またはΦ＝0.1mm以下の熱電対などを使用し、できる限り測定系の誤差を取り除いてください。特に熱電対法は強制空冷時に温度が低めに出ます。
2. 自己温度上昇ΔT_Xを実測する場合は無風状態の周囲温度TaとT_Cとの差分とし、ΔT_Xは発熱量が少なく、かつ測定値が5K以下のため測定系の影響をできる限り排除してください。
3. このような配慮をしても計算上微妙な値になる場合は詳細な計算が必要になりますがそのような場合はもっと余裕を持つべきであり、温度測定の誤差を考えると詳細計算の必要性を筆者は疑問視しています。