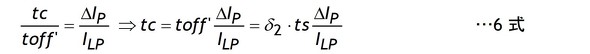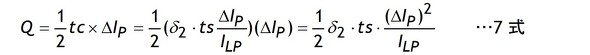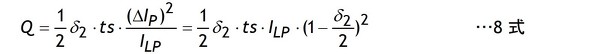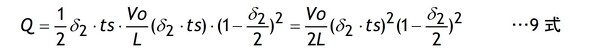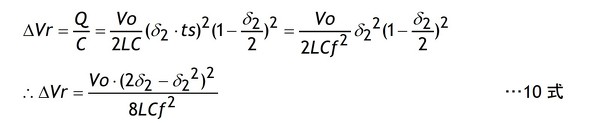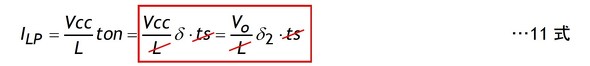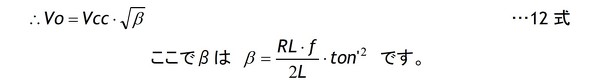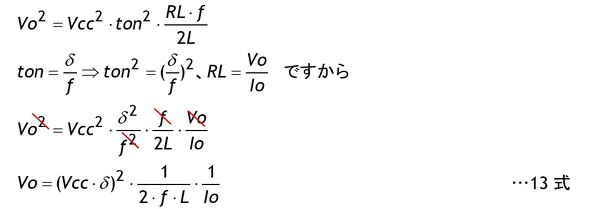反転形DC/DCコンバーターの設計（7）チョーク電流不連続時のリップル電圧計算：たった2つの式で始めるDC/DCコンバーターの設計（21）（2/4 ページ）

[加藤博二（Sifoen），EDN Japan]

2）C1の充電電荷Q

　平滑キャパシターC1がチョークL1から充電される期間は図1から分かるように、toff’期間内でチョーク電流が出力電流Ioを上回っているtcの期間内（図1水色領域）のみです。tc以後の期間はチョークから電流が供給されてもキャパシターC1の放電を緩和するのみで充電には至りません。

　一方、出力電流Ioはtoff’時間（δ₂×ts）中にチョークから放出される電流の1周期平均ですから式で表せば4式になります。

注）チョーク電流I_LはキャパシターC1を充電するとともにIoの供給源として働きます。ですから4式はキャパシター充電電流の平均値ではありません。

　そしてこのキャパシター充電電流はチョーク電流からIoを引いたものですからキャパシター充電電流のピーク値はI_LP−Io（＝ΔI_P）となり、このΔI_Pを4式とI_LPを使って表すと5式になります。

　チョーク電流I_Lとキャパシター充電電流の各波形は相似の三角形なのでtcは6式の比例則を使って求めることができます。

　充電電荷Qは図1の水色の三角形の面積（底辺×高さ÷2）であり6式のtcを使って次の7式で電荷Qを計算します。

さらに、7式のΔIpに5式の結果を代入して整理すると8式を得ます。

8式のI_LPはLの基本式や前述の3式から

です。このI_LPを8式に代入して整理すると9式を得ます。

3）リップル電圧ΔVr

　Cの基本式からリップル電圧ΔVrはキャパシターC1の電荷変動ΔQと容量Cの比ですからリップル電圧ΔVrは10式で求められます。

　10式のδ₂は1式から次のように導かれるVcc･δ＝Vo･δ₂の関係（電圧時間積）を使って求めます。

　なお10式の計算には出力電圧Voが入っているので計算に先立って12式を使ってVoを求めておく必要があります。この12式の導出については連載第18回 「反転形DC/DCコンバーターの設計（4）不連続モードの振る舞い」で説明しましたので詳しくはそちらを参照してください。

　12式を展開すると13式に示すIo-Voの関係式を得ることができます。