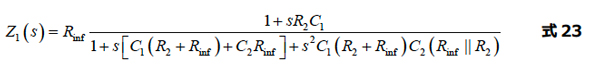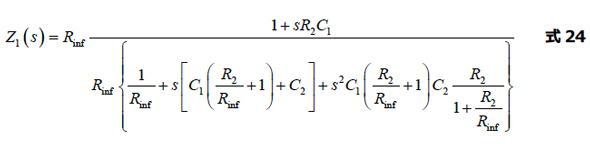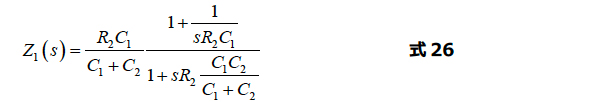オペアンプのダイナミック応答の検討(2) タイプ2補償回路の伝達関数:アナログ回路設計(7/8 ページ)
高周波時定数
これでDC時定数が得られました。次に、図20に示す高周波時定数を決定しましょう。τ21を求めるために、コンデンサーC1を短絡で置き換えると、コンデンサーC2の端子間の抵抗値に注目できます。
時定数をすぐに求めることができ、次の式で表されます。
次にτ12を求めると、次の式が得られます。
D(s)を形成する全ての項が得られました。
検討すると分子を求められます。第1部で説明したように、刺激が存在しても、変形(Cを1/sCで置き換える)後の回路網で応答が消失するsの値に設定した時点でゼロが見つかります。図18で、電流源の両端で測定したVTが応答です。VTが0Vになる時点で、回路内には必ず実質的に短絡に変形される部分が存在します。次のケースがこれに該当します。
次のケースも該当します。
これら全てを設定した後、次のような完全な伝達関数が得られます。
分母でRinfの係数を求めると、次の式が得られます。
整理して、Rinfを無限大に近づけます。最終的な式は次のようになります。
今度は分子のR2C1の係数を求めます。分母のゼロを反転した、「低エントロピー」と呼ばれる式が得られます。
次の形式で、さらに整理することができます。
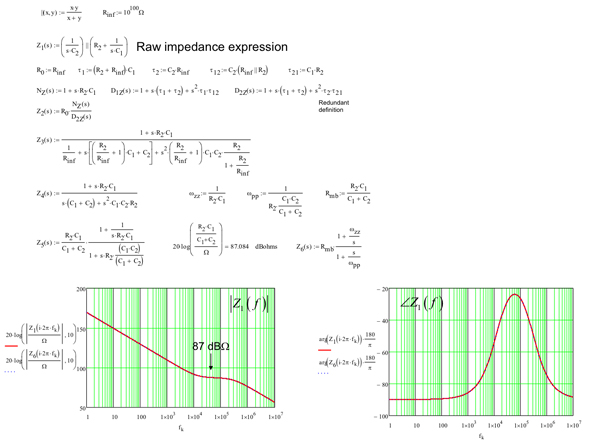
主要項(式28)は引き続き抵抗と同じ次元を使用していますが、もはやs=0に対応する値ではありません。これはプラトー領域つまり中域抵抗であり、全ての式を求め、それぞれの個別応答を検証した結果である図21で確認できます。これらはいずれも同じことを意味します。
高速分析回路手法は、回路を複数の小規模なスケッチに分解し、各スケッチを個々に解決する方法を示します。検討が可能な場合、かなり迅速に結果を求めることができ、整理された形式が得られます。これがこのアプローチの強みであり、複雑な伝達関数の決定が重要な時に時間短縮を図れるスキルを身に着けることをお勧めします。
Copyright © ITmedia, Inc. All Rights Reserved.
記事ランキング
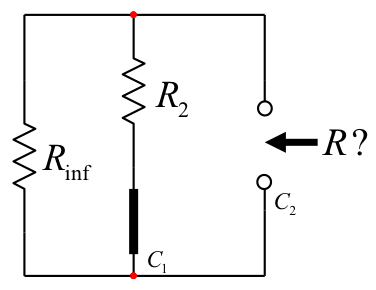 図20:コンデンサーC1を短絡で置き換えると、C2の端子間で「見られる」抵抗値はいくらか
図20:コンデンサーC1を短絡で置き換えると、C2の端子間で「見られる」抵抗値はいくらか