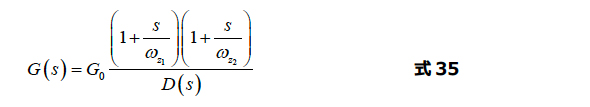オペアンプのダイナミック応答の検討（2） タイプ2補償回路の伝達関数：アナログ回路設計（8/8 ページ）

[Christophe Basso（ON Semiconductor France SAS），EDN]

タイプ3の補償回路が存在

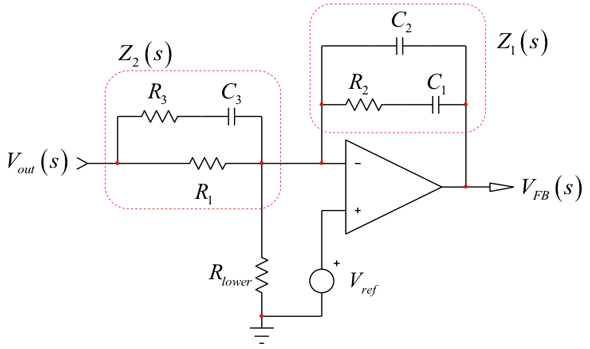
　さらに検討するために図22に注目してください。タイプ3の補償回路が存在することが分かります。1行の代数式も記述せずに、Z₁とZ₂rがそれぞれ実質上の短絡および、開路になる時に、応答V_FBが消失すると言うことができます。Z₁は式26で既に求めており、次の式で表されるゼロに寄与します。

　刺激V_outが応答V_FBを形成しないようにするには、2番目のオプションはZ₂が開路になることです。言い換えると、s＝s_z2の時にそのインピーダンスを表す式は無効になります。

図22：タイプ3の回路は3次のアクティブ・フィルター

　Z₂のインピーダンスを決定するために（この部分を全体の回路から分離する）、図18の右側のように、頭の中で電流源I_TをR₁の両端に接続することを想像します。s＝0の場合、電流源の端子間で「見られる」抵抗値がR₁です（C₃はDC状態では開路）。励起（電流源）が0Aに減少したとき（0Aの電流源は単純に回路から消失したのと同じ）の時定数は、C₃の両端から見た抵抗値RとC₃の積に等しい値です。つまり、単純にτ₃＝（R₁＋R₃）C₃となります。この場合、関心があるのは分母の根だけなので分子は必要ありません。ただし、分子も求めたい場合は、Z₁を分析したときと同じ構造になります。R₃とC₃が実質上の短絡に等しい場合、電流源の両端の応答V_Tは消失します。これらのデータを組み合わせると、次の式が得られます。

　分母を打ち消して、インピーダンスの振幅を無限大に近づけるには、次の式を解く必要があります。

　次のように変形できます。

　したがって、中間的なタイプ3の伝達関数は次のようになります。

　ここで、

および、

　D(s)を求めるには、参考資料4を参照するだけです。

---

【参考資料】
1：C. Basso, "Practical Implementation of Loop Control in Power Converters", APEC Professional Seminar, Charlotte (NC), 2015, http://cbasso.pagesperso-orange.fr/Spice.htm
2：T. Hegarty, "Error Amplifier Limitations in High-Performance Regulator Applications", AN-1997, Texas-Instruments, May 2013, http://www.ti.com/lit/an/snva411a/snva411a.pdfｋ
3：http://cbasso.pagesperso-orange.fr/Spice.htm
4：C. Basso, "Linear Circuit Transfer Functions - An Introduction to Fast Analytical Techniques", Wiley 2016, ISBN 978-1-119-23637-5