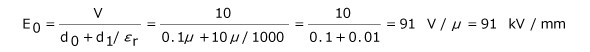セラミックキャパシター(2) ―― 誘電体とは:中堅技術者に贈る電子部品“徹底”活用講座(46)(2/5 ページ)
キャパシター内部の電界
ここで図1に示したキャパシターの内部の電界と電位分布を計算して比誘電率εrがキャパシターの内部でどのように作用しているかを確認してみます。ここで図3に示す各パラメーターは次の通りです。
d :電極間の距離(中央に誘電体)
A :電極の面積
d0:キャパシター内部の空間部分の寸法
d1:誘電体の厚み(=d-d0)
V :印加電圧
Q :与えられた電荷
図3の構造から電極間には電荷Qによる平等電界が発生するものとすると次の各式を得ることができます。
6a式から空間部の電界強度E0の極限値は、
となり、空間距離d0で印加電圧Vを受け持つことになるので電界強度E0は著しく大きくなります。一方、誘電体中の電界強度E1は6b式からεrの増加に従って減少していきます。
具体的な値をイメージするために、
d0=0.2m(0.1m×2)
d1=0.8m(d=1m)
V=1V
として比誘電率εrをパラメーターとした時の様子をグラフに表したものが図4です。
図4(a)の電位分布(電位差)を見ると比誘電率εrの増加に従って誘電体の分極が強くなるので誘電体が受け持つ電位差V1は減少する一方、空間部の分担電圧V0は逆に大きくなっていく様子が分かります。
また図4(b)に示すようにεrの増加に従って空間部の電界強度E0は増加し、誘電体部の電界強度E1は減少していきます。
積層セラミックキャパシターで積層した層が剥がれてキャパシター内部に空間(ボイド)が発生する「層間剥離」と呼ばれる現象は上記のように空間部の電界強度が増加し、限界値を超えると空間部でコロナ放電が発生して絶縁劣化につながる可能性があります。
例えば1層の誘電体厚みd1=10μの積層形セラミックキャパシターにおいて、ボイド寸法d0=0.1μ(=100n), 比誘電率εr=1000, 使用電圧V=10Vとすると空間部の電界強度E0は、
にもなり、空間のコロナ放電の電界強度(0.5〜1kV/mm)をはるかに超える値となります。
Copyright © ITmedia, Inc. All Rights Reserved.
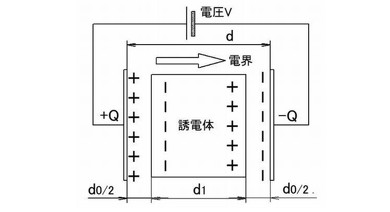 図3:キャパシター内部の関係図
図3:キャパシター内部の関係図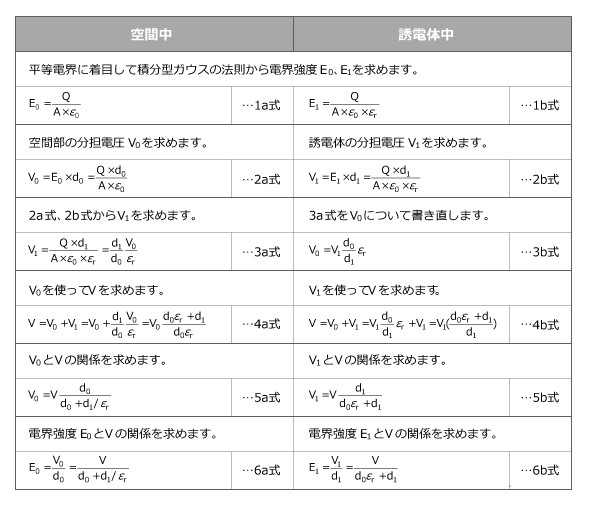

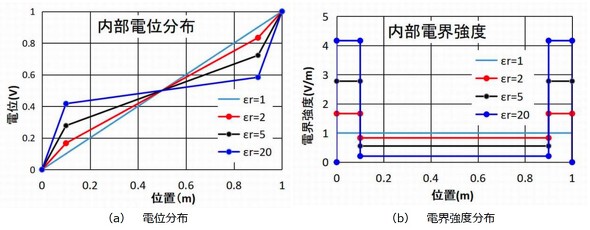 図4:比誘電率とキャパシター内部電位分布
図4:比誘電率とキャパシター内部電位分布