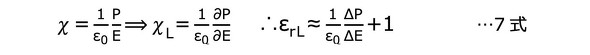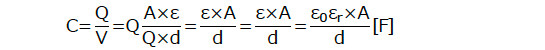セラミックキャパシター（2） ―― 誘電体とは：中堅技術者に贈る電子部品“徹底”活用講座（46）（5/5 ページ）

» 2020年08月28日 10時00分公開

[加藤博二（Sifoen），EDN Japan]

前のページへ 1|2|3|4|5 　　　　　　

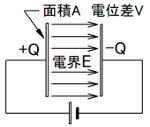
比誘電率とヒステリシス曲線

　誘電分極Pは分極率χ（＝ε_rｰ1）を用いて表すとP＝ε₀χEですが、
局所比誘電率ε_rLはPが非線形ですから、

となります。つまり図7、図8の曲線の傾きが比誘電率ε_rに関係し、垂直に近いほどε_rは大きくなります（添え字Lは局所値を表します）。

　今回は急遽、誘電体について説明をさせていただきました。次回は第1回に引き続いてセラミックキャパシターの構造の説明を行うとともに製造工程について説明をしたいと思います。

静電容量C_〔F〕を求める

　今まで単に「電気磁気学の諸式によって…」として静電容量を算出してきましたがもう少し詳細に説明します。
　右図のような平行電極（面積A)）に＋Q、－Qの電荷を与えると電極内には平等電界Eが発生します。この状態に積分形のガウスの法則、

を適用するとこの平等電界Eを表す式はE×A＝Q/εあるいはE＝Q/(A×ε)となります。また電極間の電位差はVですから

となり、静電容量Cの定義式 C=Q/Vから

となります。

（次の記事を読む）

執筆者プロフィール

加藤　博二（かとう　ひろじ）

1951年生まれ。1972年に松下電器産業（現パナソニック）に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。

⇒連載『中堅技術者に贈る電子部品“徹底”活用講座』バックナンバー

アルミ電解コンデンサー（8）―― 市場不良と四級塩問題
今回は湿式アルミ電解コンデンサーの残った課題として四級塩*問題を取り上げたいと思います。四級塩問題については現象の説明だけの資料が多く、そのメカニズムについては納得できる技術資料がほとんどありません。本稿では筆者が納得しているメカニズムを1つの説として説明をしていきます。
アルミ電解コンデンサー（7）―― 複数負荷モードでの寿命計算
今回は複数の負荷モードが繰り返される場合の機器の寿命をいくつかの負荷モードに区分して考えます。
アルミ電解コンデンサー（6）―― ドライアップ寿命
電解コンデンサーを使いこなす上で避けて通れないドライアップ寿命、いわゆる寿命について説明します。寿命設計は正しく設計しないと数年後に市場でパンクや液漏れなどの不具合を招きます。
アルミ電解コンデンサー（3）―― 化成処理と巻回
アルミ電解コンデンサーの主要部材であるアルミ箔。今回は、エッチングされた箔の表面に施す化成処理について詳しく説明していきます。
アルミ電解コンデンサー（2）―― 箔の様子
今回はアルミ電解コンデンサーのキーパーツの1つである箔（はく）の様子について詳しく説明していきます。
アルミ電解コンデンサー（1）―― 原理と構造
今回から、湿式のアルミ電解コンデンサーを取り上げます。古くから、広く使用される“アルミ電解コン”ですが、さまざまな誤解、ウワサ話があるようです。そこで、誤解やウワサに触れつつ、アルミ電解コンの原理や構造、種類などを説明していきます。